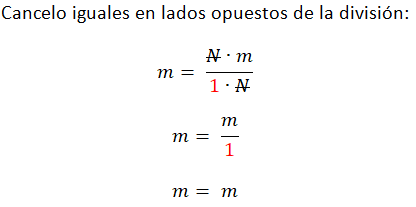Análisis dimensional

Hay dos tipos de análisis dimensional, a nivel de secundaria es más recomendado abordar este tema solamente usando las unidades de medida del S.I.

Analizar dimensionalmente es escribir una fórmula y en lugar de sustituir con números, sustituir con unidades o dicho en otras palabras es trabajar con unidades para buscar o llegar a la unidad que necesitas de la fórmula.

El análisis dimensional es una herramienta poderosa en física, principalmente cuando hacemos despejes y queremos comprobar si el resultado está correcto o cuando inventamos una fórmula a partir del razonamiento, pues haciendo el análisis respectivo puedes darte cuenta si es correcta la unidad obtenida.

Seguramente ya estás deseoso de aprenderlo; entonces, veamos.

En palabras simples hacer un análisis dimensional es probar mediante las unidades que la fórmula o el despeje es correcto, en los siguientes ejemplos usaremos fórmulas que ya hemos despejado y son evidentemente, correctas, pero tome nota que esta es una herramienta para confirmar si es o no correcta. Por eso siempre al final de una A.D. (análisis dimensional) debes obtener una igualdad, por ejmple: kg=kg o m=m.

Hay ciertas reglas que facilitan hacer A.D.:

a +a = a    esto se cumple porque trabajamos con magnitudes, por ejm 1m+1m = 2m o -5m+5m= 0m
a – a = a    esto se cumple porque trabajamos con magnitudes, por ejm 30m-5m = 25m o 5m-5m= 0m
a . a = a²

También siempre que trabaje con fracciones, no las escribas así:

m/s²

sino

Finalmente, si una fórmula incluye números, o constantes como pi, estas no se usan, ni siquiera se incluyen en el A.D.

Análisis dimensional en el tema de MRUA:

Haremos el análisis dimensional para la siguiente fórmula:

Veamos otro ejemplo esta vez con esta fórmula:

Podemos ver otrso ejemplos en otro tema seguidamente:

Análsis dimensional en el tema de fuerza elástica:

En una fórmula como la siguiente:

Al final obtenemos una igualdad (kg=kg) y es lo que se busca.

Ahora hagamos otro análisis  dimensional para que veas que es fácil, hagamos el análisis dimensional de ΔX de la fórmula de fuerza elástica:

ΔX = F
         k

1) Debemos primero conocer a qué unidad queremos llegar, como buscamos ΔX, que es cambio de longitud; entonces, buscamos metros.

2) Sustituimos cada variable por la unidad en que se mide: