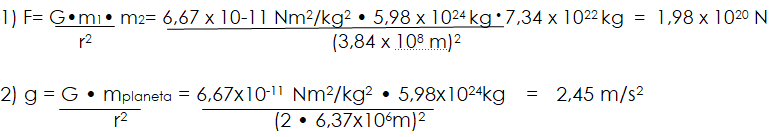Cuarta Ley de Newton: Ley de la Gravitación Universal

Otros científicos antes de Newton estudiaron el movimiento de los planetas y hasta dedujeron que la Tierra gira alrededor del Sol y la Luna alrededor de la Tierra, dedujeron las leyes que dominan estos movimientos; pero, faltaba que alguien explicara la razón de que los cuerpos del universo se mantuvieran ordenadamente unidos, ¿qué hacía que la Tierra girara alrededor del Sol o la Luna alrededor de la Tierra? ¿por qué la Tierra no seguía su curso en línea recta? Newton fue quien dio estas respuestas, él dedujo que a los planetas los mantenía unidos una fuerza a la cuál denominó Fuerza de atracción gravitacional.

 

 

F= Fuerza de atracción gravitacional; se mide en N   m1= Masa de un cuerpo; se mide en kg                                    m2= Masa del otro cuerpo; se mide en kg r = radio o distancia que los separa; se mide en m G= constante gravitatoria: 6,67X10-11 Nm2/kg2

El campo gravitatorio de un planeta es la zona del espacio donde la gravedad del planeta en una masa cualquiera origina una fuerza, de modo:

g = F/m

 

Como ya conoces, el peso es una fuerza producto de la gravedad del planeta.

Por esa razón podemos hacer una demostración y obtener una nueva fórmula de gravedad, relacionando estas dos fórmulas:

Peso	Fuerza gravitacional
p=m.g

 

Entonces siga estos pasos para obtener una nueva fórmula de gravedad:

1. 1. Busque la(s) fórmula(s) que se aplica(n) al caso de acuerdo con los datos.
   2. Despeje una variable que NO le den en el ítem y sea igual en ambos casos.
      Aquí peso es igual que fuerza gravitacional, de modo que ya están los despejes.
   3. Elabore una igualdad sustituyendo con las variables del ítem.
      Aquí solo iguale ambas ecuaciones: m.g=G.m1.m2/r²
   4. Resuelva lo que le piden despejando.

Video de la demostración:

Escriba su demostración aquí:

 

Antes de continuar compare su resultado con el que aparece en las respuestas.

En la nueva fórmula obtenida note que el radio está abajo, de modo que entre más nos alejamos de la superficie del planeta, menor es la gravedad, y entre más nos acerquemos, mayor es su gravedad, y en efecto esto sucede en la Tierra, la gravedad en las montañas es algo menor que en la costa del mar donde su valor es el mayor. Pero, contrario a lo que se pensaría desde la superficie de la Tierra y hasta el centro, la gravedad disminuye hasta hacerse cero en el centro de la Tierra.

En los siguientes ejemplos y práctica, debemos suponer que los planetas tienen la masa uniformemente distribuida en su superficie.

Cuadro: DATOS DEL SISTEMA SOLAR PARA REFERENCIAS POSTERIORES

Cuerpo	Radio   (km)	Radio de la órbita (Km)	Masa   ( kg )	Densidad   ( kg /m³)	Satélites   Conocidos	Gravedad en la superficie (m/s²)	Período de la órbita (Años)	Período de Rotación (Días)
Mercurio	2450	5,79 x 107	3,28 x 1023	5600	–	3,6	0,241	58
Venus	6050	1,08 x 108	4,83×1024	4860	–	8,9	0,615	243
Tierra	6370	1,49×108	5,98×1024	5500	1	9.8	1	1
Marte	3350	2.28×108	6.40×1023	4000	2	3.8	1,882	1.2
Jupiter	69000	7.78×108	1.9×1027	1300	16	26.6	11.86	0.41
Saturno	59250	1.43×109	5.68×1026	700	17	10.8	29.46	0.43
Urano	23450	2.87×109	8.67×1025	1500	15	10.5	84.1	0.45
Neptuno	22250	4.49×109	1.5×1026	1700	8	14.2	164.7	0.66
Plutón	1150	5.93×109	1.8×1022	2100	1	0.9	248.9	6.4
Sol	696000	1.92×1016	1.98×1030	1400	9	272.6	2×108	25.5
Luna	1740	3.82×105	7.34×1022	3320	–	1.6	27.33 días	27.33

Nota: Los datos de período de la órbita del Sol son alrededor del centro de la Vía Láctea, y los de la Luna alrededor de la Tierra.

Práctica de Cuarta Ley de Newton.

Elabore el análisis dimensional de cada fórmula aplicada.
Recuerde análisis dimensional: https://www.fisicalinda.com/courses/la-caja-de-herramientas/lessons/analisis-dimensional/ 

1) ¿Cuál es la fuerza de atracción entre la Tierra (5,98X10²⁴kg) y la Luna (7,34X10²²kg), si los separa una distancia de 3,84X10⁸ m entre sus centros?  Suponga que son cuerpos homogéneos.

 

 

 

2) ¿Cuál es la gravedad de la Tierra a una distancia, desde el centro, de dos radios terrestres, si el radio terrestre es 6,37×10⁶m?

 

 

 

 

 

3) ¿Cuál es la fuerza de atracción gravitatoria entre usted y su compañero más cercano? Compárela con la fuerza de atracción gravitatoria entre la Tierra y la Luna.

 

 

 

 

4) Dos carros de 1000 kg cada uno se atraen con una fuerza gravitacional de 7,41×10^-6N ¿Han chocado estos carros o están separados uno de otro?

 

 

 

 

5) ¿Cuál es la fuerza de atracción entre la Tierra y el Sol si los separa una distancia de 1,49×10⁸ km?

 

 

 

 

6) Calcule la gravedad de la Luna si tiene un diámetro de 3475km.

 

 

 

7) ¿Con cuánta fuerza atrae la Tierra a un astronauta de 80kg que está a 500km sobre la superficie terrestre?

 

 

 

 

 

8) Entre la Luna y un cuerpo existe una fuerza de atracción de 2×10¹⁰N ¿qué masa tiene este cuerpo si está a 400km de distancia de la superficie lunar?

 

 

 

 

9) Un planeta con una gravedad de 18m/s² tiene un radio de 5×10⁷m ¿cuál es su masa?

 

 

 

 

 

 

10) Actividad de cierre:

Proceso:
1) Busca una bola de hacer ejercicios, de unos 80 cm de diámetro que representaría al Sol.

2) La Tierra sería una bolita de 0,7 cm a 86 m de distancia.

3) Calcule la fuerza de atracción gravitacional entre ambos.

Nota para el docente: Esta actividad se puede ampliar tal como se explica aquí: https://www.fisicalinda.com/lessons/didactica-para-el-cierre-de-iv-ley-de-newton/

 

Respuestas:

Demostración para obtener la fórmula de gravedad.   p= m.g Ya que el peso es una fuerza puedo en vez de F sustituir por m.g     Respuestas para el resto de la práctica: 3) Nunca, porque es muy poca. Todas las respuestas serán diferentes; pero, el exponente debe estar entre 6 y-7. Y la fuerza Tierra Luna está en el ejemplo resuelto. 4) Están separados uno de otro 3m. 5) 3,55×1022N 6)1,62m/s2 7)676N 8)1,86×1010kg 9) 6,74×1026kg

 

Pero no podemos terminar este tema sin ampliar un poco los conceptos.

En primer lugar, de un análisis detallado del cuadro de datos del sistema solar, se observa que el Sol también tiene periodo de rotación y radio, ya que el sol orbita al eje galactico, el movimiento real del sol es algo así como esta animación:

Pero eso no es todo, la masa de Júpiter es tan grande, que los planetas no giran en torno al Sol, sino al centro de masa del sistema solar, un baricentro ubicado en el vacío, tal como se muestra en esta animación:

Práctica final de IV Ley de Newton: