El álgebra vectorial
Cálculos con vectores
El álgebra vectorial es una herramienta matemática poderosa, en Física se usa mucho, y para usarla, por lo menos se debe conocer algunos conceptos relevantes enumerados seguidamente.
Video:
PRIMER CASO. VECTORES CONSECUTIVOS:
Los vectores consecutivos son aquellos que están dispuestos en una sola línea, por ejemplo:
![]()
Por ejemplo: Juan empuja la mesa hacia adelante y Carlos la hala hacia adelante, esos son dos vectores consecutivos.

Para sumar dos vectores consecutivos simplemente se adicionan sus valores y se da el sentido del mayor.
Pero esta regla aplica únicamente si el observador está afuera del sistema.
Para resolver exitosamente los problemas de este tema debes:
Primeramente, pensar adónde está el observador, ¿adentro o afuera del sistema?
1) Para un observador afuera del sistema y que está en reposo: Él ve las velocidades “reales” que los cuerpos tienen.
2) Para un observador adentro del sistema: Desde su punto de vista lo que se mueve y cambia es el mundo que lo rodea, nunca él mismo, por ejm;
¿has visto la Luna cuando vas en un vehículo?
¿verdad que de niños pensábamos que la Luna nos perseguía?
Eso es una prueba de que, desde la perspectiva de un observador adentro de un sistema, lo que cambia es el mundo, no el mismo, la velocidad propia él se la asigna al otro cuerpo.
Estudiemos los siguientes ejemplos de suma de vectores consecutivos.
Ejemplo 1:
| Un río tiene una corriente cuya velocidad es de 1 m/s y una persona nada en él a una velocidad de 2 m/s y hacia abajo, en la misma dirección que la corriente del agua; ¿a que velocidad ve un observador en la orilla a el nadador en el río? |  |
Respuesta: Para averiguar este valor de velocidad, es necesario notar que el observador está afuera del sistema y sumar ambas velocidades, así de simple
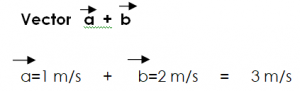
Resultado: La persona viaja a 3 m/s hacia abajo en la misma dirección que la corriente de agua.
Ejemplo 2: Un río tiene una corriente cuya velocidad es de 1 m/s y una persona nada en él a una velocidad de 2m/s y en sentido contrario a la corriente del agua; responda:
a) ¿a cuál velocidad ve un observador en la orilla al nadador en el río?
Respuesta: Éste es similar al anterior, nuevamente el observador está afuera del sistema, ahora se restan los valores debido a que ambas velocidades son opuestas. Esto se representaría así:

Nota: Quizá algunos están pensando que si van en la misma dirección se suma y si van en direcciones opuestas, esta regla solo aplica si el observador está afuera del sistema, pero si está adentro del sistema NO aplica, como prueba estudie el siguiente caso.
b) Ahora el nadador viaja en sentido contrario al agua, ¿a cuál velocidad ve el nadador (que viaja a 2 m/s) a una hoja que viene siendo arrastrada por la corriente del río a la misma velocidad que la corriente de agua (1 m/s)?
Respuesta: En este caso, el observador es él mismo, está adentro del sistema, de modo que ve a la hoja acercarse con la velocidad del río (la hoja viene a la misma velocidad que la corriente de agua 1m/s) más la velocidad de él mismo:

SUMA DE VECTORES EN DIFERENTES LÍNEAS DE ACCIÓN
Los vectores también se pueden presentar en diferentes líneas de acción, por ejemplo:
Juan camina 4 m al norte y luego 5 m al este. O bien, una mosca vuela 2 m a 45° y 4 m a 60° y 6 m a 150°.
En tales casos los vectores se suman siguiendo el mismo proceso, se agregan a un eje de coordenadas cartesiano y se suma respectivamente aplicando Pitágoras o trigonometría.
Estudiemos esta situación:
María jala la mesa al Sur con 2 N de fuerza, y Juan la jala hacia el al Este con 3 N de fuerza. ¿Cuál es la fuerza resultante y respecto a Juan en qué ángulo se desvía?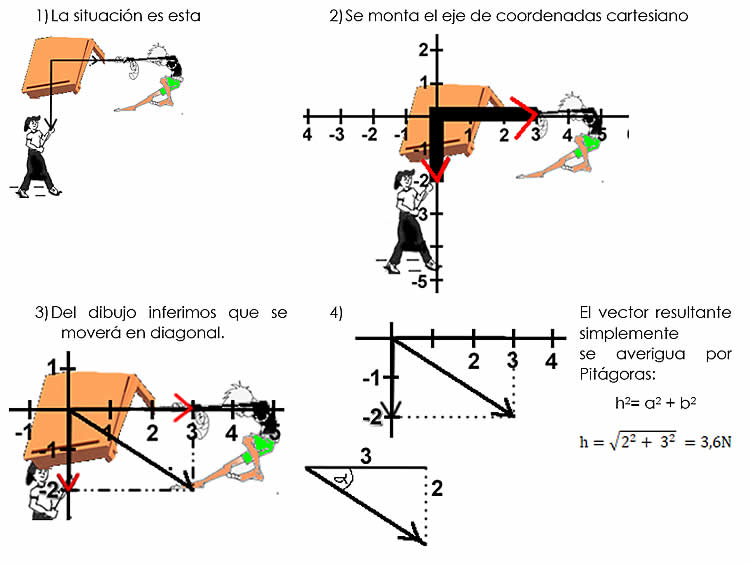
Y si desea averiguar el ángulo respecto a la horizontal en que está dirigido el vector resultante,
Solo observe que se forma un triángulo con un cateto de 2N y otro de 3N e hipotenusa de 3,6N, de modo que puede aplicar cualquier función trigonométrica, recuérdelas:
| Sen α = Cateto opuesto Hipotenusa | Cos α = Cateto adyacente Hipotenusa |
Tan α = Cateto Opuesto Cateto Adyacente |
Con los datos del triángulo aplicaremos seno (usted puede aplicar cualquier otra función) y para averiguar directamente el ángulo sacamos directamente el seno inverso así:
Sen -1 ∂ = Cateto opuesto = 2 = 33,74°
Hipotenusa 3,6
Existen situaciones, llamadas “suma de vectores perpendiculares consecutivos”, son aquellos a donde los vectores son perpendiculares entre sí pero que la cola de uno va con la punta del otro, por ejemplo: María empuja la mesa al Sur con 2N, y Juan la jala hacia el al Este con 3 N.
Si los vectores son dirigidos consecutivamente, puede aplicar las mismas reglas, vea el siguiente ejemplo, que aplica lo mismo de arriba, pero de forma resumida:
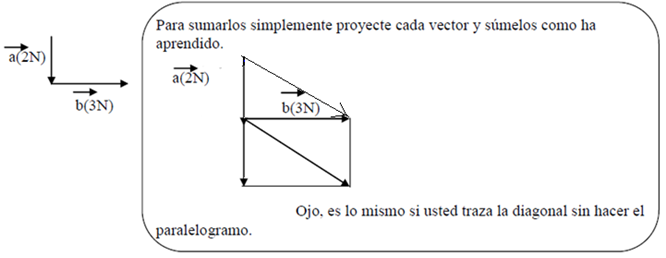
Existen otras características de los vectores, pero ya que no las usaremos por ahora, serán vistas más adelante.
Puedes ver sumas más complejas resueltas por el método descrito en este sitio:
Ok, ahora veamos un ejemplo del método de construcción de un paralelogramo para la suma de vectores.
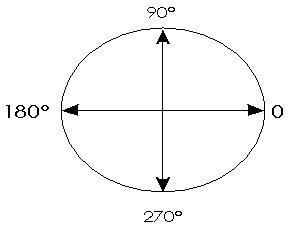
Un concepto que debes recordar es el círculo trigonométrico del cual se deduce que los ángulos se miden de derecha a izquierda.
Ejemplo 1:
Vídeo que explica el primer ejemplo:
La siguiente representación son 5 vectores en un eje de coordenadas cartesiano (x, y): si la cuadrícula representa 1 m cada cuadrito, averigüe la magnitud de cada vector:
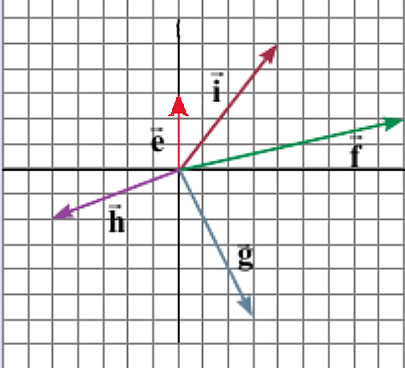
Este ejercicio explica cómo sumar varios vectores en diferentes ángulos.Suma de varios vectores
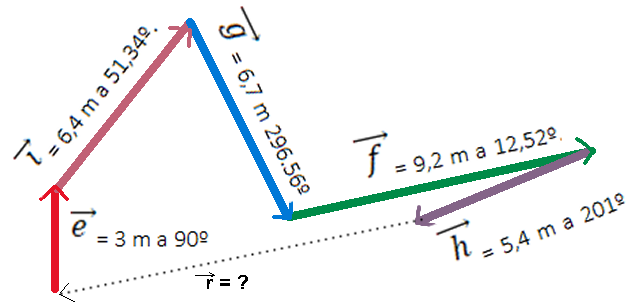
Averigüe a qué distancia quedaron de la entrada de la cueva (averiguar vector ![]() ).
).
Nota de solución:
Para hacer esta suma de vectores debes averiguar las componentes X, Y de cada vector y sumarlas por aparte, si te fijas bien, puedes usar como referencia el ejercicio anterior y medir las componentes en el eje de coordenadas cartesianas; ya que son los mismos vectores, pero es común en este tipo de ejercicios que debas averiguar las componentes por ti solo, así es que veremos cómo:
| Cálculo de cada componente | Suma de las componentes | ||||||
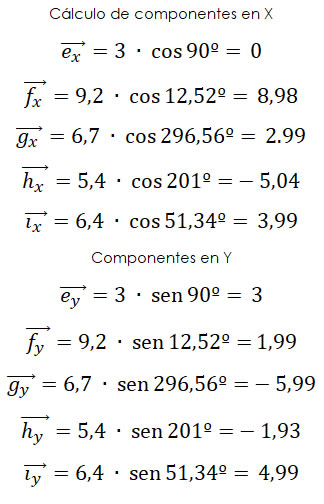 |
Ahora, tenemos una sola magnitud en X y una sola en Y, de modo que podemos construir un triángulo con esos dos valores y si averiguamos la hipotenusa conseguimos la magnitud de la longitud desde donde quedaron hasta la entrada de la cueva, y el ángulo se consigue por trigonometría. Por lo tanto se encuentran a una longitud de 11,11m de la entrada, y deben desviarse en un ángulo 196,8º. |
¿PARA QUÉ SON ÚTILES LOS VECTORES?
Los vectores nos ayudan en dibujo gráfico, medición de fuerzas, animación digital (como al diseño de juegos de vídeo), direccionamiento de satélites, etc… Y muy importante: Para que aprendan razonamiento abstracto y geoespacial. 😉
El cálculo vectorial es la base para toda ingeniería y la arquitectura, una situación que requiere cálculo vectorial puede ser analizada en la siguiente demostración donde tienes unas pesas que se suspenden de tres cuerdas unidas. Dos de las cuerdas pasan sobre poleas sin rozamiento. Las tres fuerzas que actúan sobre el nudo (flechas coloreadas) están en equilibrio.
Por ahora solo mira cómo las fuerzas varían el paralelogramo y por tanto el vector de la fuerza resultante:
Práctica.
La práctica se encuentra al final, ahora solo se presentan dos ejercicios (7 y 8) que son diferentes de la práctica final.
7) Por qué es indispensable el uso de vectores en el funcionamiento de una app como Waze, el GPS o Google street para la geolocalización.
- a) porque la tecnología es muy compleja.
- b) porque las computadoras realizan cálculos complejos siempre.
- c) son necesarias direcciones y tamaños para dar una posición exacta.
- d) se necesitan números exactos para poder dar posiciones exactas.
8) Las abejas, mariposas, palomas nocturnas, abejones y otros se orientan mediante la luz del sol, la luna o estrellas, con sus ojos ellos polarizan la luz y calculan el ángulo de su punto de partida, se trasladan en el espacio y si necesitan regresar a su origen, hacen los cálculos pertinentes y regresan calculando el vector de retorno. Claro, ellos hacen una suma de vectores en tres dimensiones (x,y,z) y es un poco más que lo que hemos visto, pero nosotros la haremos solo en x, y. Imaginemos que somos una abejita que salió de su panal en la base de un árbol y lo único que hizo fue subir unos cuantos metros para tomar el néctar de 4 flores en lo alto del árbol, y luego regresar al panal. Si se movió como lo describe la figura, ¿a qué ángulo debe moverse la abejita y cuánta longitud deberá recorrer para llegar a su panal?
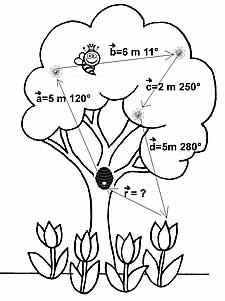
La lección termina con la solución de la siguiente prueba de conocimientos:
