El movimiento relativo
Respuestas: Carlos mira a Juan: -10 km/h. María a Carlos: 0 km/h. Pepito los ve a sus velocidades respectivas 6º km/h y 50 km/h.
Mira este video que te explica el tema:
¿Entiende por qué para hablar de movimiento primero hay que decir respecto a qué?
Lo que debemos hacer es definir algún marco de referencia que es una posición fija para todo observador y se da cualquier descripción de movimiento en referencia a este marco.
También cuando decimos que algo se está moviendo, la primera pregunta es ¿respecto a qué?, y al definirlo estamos hablando del marco de referencia.
Ejemplos de cómo podemos usar marcos de referencia para dar una descripción, podemos decir que usted está 3m norte y 4 m este de la puerta del aula. Que el carro azul se mueve a 60 km/h respecto a un observador en la calle, no respecto a otro carro en movimiento.
Al hablar de un marco de referencia; entonces, podemos definir las posiciones exactas.
Ahora por favor haga uso de los conocimientos de suma de vectores consecutivos y de movimiento relativo, recuerde pensar en dónde está el observador, adentro o afuera del sistema y responda la siguiente práctica.
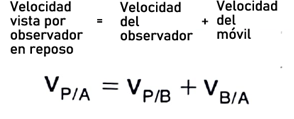
Para hacerlo muy simple veremos esta fórmula que aparece así mismo en la prueba FARO:
Es válida para un observador que está afuera del sistema:
Esta siguiente fórmula NO aparece en FARO, pero es muy fácil de recordar y se aplica para un observador adentro del sistema:
V = Vcuerpo – Vobservador
Estudiemos los ejemplos vistos anteriormente en el tema de vectores, pero ahora resueltos con las fórmulas:
|
1) Un río tiene una corriente cuya velocidad es de 1 m/s y una persona nada en él a una velocidad de 2 m/s y hacia abajo, en la misma dirección que la corriente del agua; ¿a que velocidad ve un observador en la orilla a el nadador en el río? |
 |
Como el observador está afuera del sistema:
En este caso tenemos un observador y dos móviles, por eso modificamos la fórmula para tres cuerpos:
V = 0 m/s + 1 m/s + 2 m/s = 3 m/s
V = Velocidad del Observador + Velocidad del agua + velocidad del nadador.
2) Un río tiene una corriente cuya velocidad es de 1 m/s y una persona nada en él a una velocidad de 2m/s y en sentido contrario a la corriente del agua; responda (Observe que este problema tiene pregunta a y pregunta b, ambos tienen el mismo enunciado):
- a) ¿a cuál velocidad ve un observador en la orilla al nadador en el río?
Como el observador está afuera del sistema:

En este caso tenemos un observador y dos móviles, por eso modificamos la fórmula para tres cuerpos,
note que los signos van de acuerdo con los ejes cartesianos:
V = 0 m/s + 1 m/s + -2 m/s = -1 m/s
V = Velocidad del Observador (el está en reposo) + Velocidad del agua + velocidad del nadador (negativa porque va contracorriente).
- b) Ahora el nadador viaja en sentido contrario al agua, ¿a cuál velocidad ve el nadador (que viaja a 2 m/s) a una hoja que viene siendo arrastrada por la corriente del río a la misma velocidad que la corriente de agua (1 m/s)?
Por fórmula, como el observador está adentro del sistema:
V = Vcuerpo A – Vobservador.
V = -1 m/s – 2 m/s = -3 m/s
Le asignamos el negativo a la hoja porque desde la perspectiva del observador el la ve en sentido opuesto a él mismo, la ve que se acerca. Si la viera alejarse, sería positiva.
PRÁCTICA
1) Un bus viaja hacia el Norte a 10m/s y un hombre dentro del bus camina a 2m/s hacia el Norte, ¿Cual es la velocidad del hombre observada por un espectador en la calle?
Solución por fórmula:
- VP/A= VP/B + VB/A
- VP/A= 0 m/s + 10 m/s + 2 m/s= 12 m/s
Solución por lógica:
2) Un bus viaja hacia el Norte a 10m/s y un hombre dentro del bus camina a 2m/s hacia el Sur. ¿cuál es la velocidad del hombre observada por un espectador en la calle?
Solución por fórmula: VP/A= 0 m/s + 10 m/s + -2 m/s= 8 m/s
Solución por lógica:
3) Un vehículo rojo viaja a 60 km/h y persigue un carro azul que viaja a 50 km/h.
a) ¿A qué velocidad ve el hombre del carro azul al carro rojo?
Solución por fórmula:
- Observador adentro del sistema:
V = Vcuerpo A – Vobservador= 60 km/h – 50 km/h = 10 km/h al encuentro.
B) ¿A qué velocidad ve el hombre del carro rojo al carro azul? Explicación.
Solución por fórmula: V = Vcuerpo A – Vobservador= 50 km/h – 60 km/h = -10 km/h hacia atrás, en retroceso.
C) ¿Qué rapidez mide un tráfico en la calle para el carro rojo y al carro azul?
Solución por fórmula:
- Observador fuera del sistema:
Carro azul: VP/A= VP/B + VB/A - VP/A= 0 m/s + 50 km/h= 50 km/h
- Carro Rojo: VP/A= VP/B + VB/A
- VP/A= 0 m/s + 60 km/h= 60 km/h
4) Un carro va al Norte a 60km/h y otro viaja al Sur a 50km/h, ¿A qué velocidad ve el hombre de un carro acercarse el otro?
Solución por fórmula:
- Observador adentro del sistema:
Suponiendo que el observador está viajando a 60 km/h - V = Vcuerpo A – Vobservador= -50 km/h – 60 km/h = -110 km/h.
El signo negativo, solo indica que el observador lo ve al encuentro.
Solución por lógica:
Práctica de profundización
1) Un Policleto corre a 15 Km/h tras un sospechoso que huye en bicicleta a 14 km/h, ambos se mueven en línea recta hacia el este, la velocidad del guardia con respecto al perseguido es
a) 15 km/h al oeste
b) 1km/h al oeste
c) 15 km/h al este
d) 1km/h al este
Ayuda:
2) Un vehículo viaja hacia el norte a 50 km/h; a la vez otro vehículo se mueve detrás de él, hacia el norte a 60 km/h. El segundo vehículo se mueve con respecto al primero a una velocidad de
a) 110 km/h norte
b) 60 km/h norte
c) 10 km/h norte
d) 10 km/h sur
Solución:
3) Sobre la plataforma de un vagón que viaja a 40 km/h se mueve una persona a 5km/h en la misma dirección. Para un observador que se encuentra en tierra y en reposo, la persona se mueve con una rapidez de
a) 5 km/h
b) 35 km/h
c) 40 km/h
d) 45 km/h
Explicación:
4) Dos automóviles corren uno hacia otro por un camino rectilíneo. El primero se dirige hacia el sur a 40 km/h y el segundo hacia el norte a 30 km/h. La velocidad del primero con respecto al segundo es
a) 70 km/h sur
b) 40 km/h sur
c) 70 km/h norte
d) 40 km/h norte
Explicación:
5) Un autobús se desplaza hacia el este, con velocidad Va. Una mosca se desplaza de la parte delantera a la trasera del autobús con velocidad Vs. Si nos situamos en reposo fuera del autobús al lado de este, y sabiendo que Va es mayor que Vs, la velocidad de la mosca con respecto a nosotros es
a) Vs, hacia el oeste.
b) Va, hacia el oeste.
c) Va-Vs, hacia el este.
d) Va+Vs, hacia el este.
Explicación:
Práctica para examen de Movimiento Relativo:


Excelente metodologia amigo. Un verdadero profesional en el àrea de la fisica. 100%.
Gracias.
excelente trabajo, súper explicado.