Después de la introducción didáctica que ha realizado el docente (se sugiere esta: https://www.fisicalinda.com/lessons/introduccion-didactica-al-mcu/ )
Video de la clase:
Una partícula tiene movimiento circular cuando gira alrededor de un eje, describiendo la trayectoria de una circunferencia, es lo mismo que hace una piedra cuando está girando atada por un hilo, si además tenemos que la magnitud del valor de velocidad no varía; entonces, el movimiento es uniforme.
Cuando observamos una partícula girando con MCU, al tiempo que la partícula tarda en dar un giro completo se le denomina período y se representa con la letra T; pero, al número de vueltas que da por unidad de tiempo, se le denomina frecuencia y se representa con una f; estos dos conceptos se relacionan así:
| Variable | Significado | Definición | Unidad | Ejemplo | Fórmula |
| f | Frecuencia | Número de vueltas en 1 s. | Hertz: Hz (Vuelta/s) |
f=2 HZ significa que da 2 vueltas en un segundo | 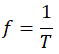 |
| T | Período | Tiempo en dar 1 Vuelta. | Segundo | T= 2s.
Significa que dura 2s en dar una vuelta |
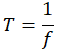 |
Si una piedra gira en MCU y la cuerda se rompe, la piedra saldría disparada con velocidad tangencial, que es una velocidad dirigida en forma tangencial a la trayectoria.
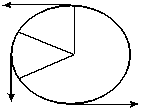 La velocidad tangencial siempre es dirigida en forma tangencial a la trayectoria (que es circular). Esta velocidad cambia continuamente de dirección; pero, no de magnitud (valor). La velocidad tangencial siempre es dirigida en forma tangencial a la trayectoria (que es circular). Esta velocidad cambia continuamente de dirección; pero, no de magnitud (valor). |
El cálculo de la velocidad con que viajaría si fuera soltada (velocidad tangencial) se hace con:
o
|
r= radio, se mide en m
V= Velocidad tangencial lineal, se mide en m/s. T= Período, se mide en s. f= Frecuencia, se mide en Hz. |
Veamos algunos casos que les ayudaran a aplicar lo aprendido:
1) Una partícula da 500 vueltas por hora, su frecuencia en Hz es la siguiente:
2) Una partícula da 500 vueltas por hora, ¿Cuál es su período en segundos?
3) Un niño tiene una piedra amarrada a una cuerda de Nylon de 1m, él mide y nota que dura 15 s en dar una vuelta completa; entonces, suelta la cuerda y la piedra salió disparada, tú decides asombrar al niño con los conocimientos que adquiriste en lecciones de física, así es que le dices que la velocidad que adquirió en el momento en que fue soltada es la siguiente _____________
4) En un experimento Carlos nota que una partícula gira con un período de 3s y Pedro mide la velocidad en su periferia obteniendo que es de 15 m/s; entonces, ellos buscan un físico que les ayude a averiguar el radio en que gira y apareces tú, quien lo calcula y les dice que es el siguiente _____________
Nota. Debe despejar radio de una fórmula.
Respuestas:
1) Una buena idea es resolverlos por regla de tres. Tema visto desde la escuela; Por ejemplo si te dicen: un chayote cuesta 5 colones ¿cuánto cuestan 6 chayotes? Se plantea así
1Mango 6 Mangos Se multiplica en cruz y se divide entre lo que sobra
5 colones x colones y da como resultado x = 30 colones. ¡EUREKA!
En la regla de tres (Que NO es factor de conversión) horizontalmente hay que tener cuidado de que todo sea igual, o sea mangos con mangos, y colones con colones en el mismo renglón, al revés sucedía con el factor de conversión, por eso se enfatiza que son diferentes.
Entonces aplicando una regla de tres a este problema tendremos:
500 vueltas
1 hora
Pero si observas te van a pedir el resultado en Hz o sea vueltas/segundo, entonces desde ahora puedo decir
500 vueltas x vueltas x= 1 x 500 = 0,13888 vueltas en 1 segundo = f
3600 segundos 1 segundo 3600
Redondeando este 0,1388 puedo decir que tiene 0,14 hz de frecuencia.
2) Este lo podemos solucionar con fórmula o con regla de tres, inicio con regla de tres.
Respuesta:
Recordemos primero que un período es el tiempo en dar una vuelta por lo tanto me están pidiendo cuánto tiempo dura en dar una vuelta, por eso planteo la regla de tres así
500 vueltas 1 vuelta entonces x = 1 x 3600 = 7,2 s = T
3600 segundos x segundos 500
Resolviéndolo con fórmula, simplemente aplico
T = 1 = 1 = 7,14 s
f 0,14 Hz
¡Hey! pero mire que los dos resultados son diferentes, pues sí, sucede que en física tenemos que acostumbrarnos a obtener resultados aproximados pues los decimales a veces nos toman el pelo, el primer resultado es el más exacto. El segundo (7.14s) es más inexacto pues lo obtuvimos al dividir entre el resultado del ítem anterior; pero, si en lugar de dividir entre 0,13 hubiéramos usado todos los decimales 0,13888888, ambos resultados serían iguales. ¿Cuál es el correcto? Ambos son correctos.
3) 0,41 m/s
4) 7,16m.
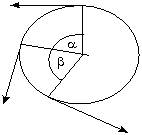
Pero existe una velocidad con la cual gira recorriendo los ángulos, y se denomina velocidad angular, se mide en radianes por segundo (rad/s) y es dada por:
| r= radio o distancia al eje, se mide en m.
w= velocidad angular, se mide en rad/s. V= velocidad tangencial, se mide en m/s. T= período, se mide en s. αy β = ángulos recorridos. Nota: Los radianes son otra forma de medir los ángulos. 180° corresponden a ¶ radianes y entonces 360 = 2 ¶ rad. |
|
 |
Del movimiento circular uniforme, sin cambio en la magnitud de la velocidad, resulta una 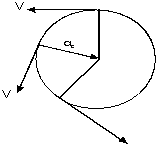 aceleración tangencial nula; pero, como la partícula a cada instante está cambiando de dirección, continuamente está teniendo una aceleración centrípeta (dirigida hacia el centro) dada por
aceleración tangencial nula; pero, como la partícula a cada instante está cambiando de dirección, continuamente está teniendo una aceleración centrípeta (dirigida hacia el centro) dada por
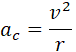 |
ac= aceleración centrípeta, se mide en m/s2. |
Elabore las siguientes dos demostraciones, recuerde los pasos:
Tu respuesta aquí:
2) Sabiendo que la circunferencia de un círculo es ![]() , y que la rapidez en el MRU es
, y que la rapidez en el MRU es ![]() demuestre que la siguiente ecuación es correcta:
demuestre que la siguiente ecuación es correcta:
![]()
1) Saque los datos y la incógnita, para distinguir los datos te será muy útil usar el siguiente cuadro.
| Símbolo | Variable | Significado | Unidad |
| f | Frecuencia | Número de vueltas por segundo | Hz |
| T | Período | Tiempo en dar una vuelta | s |
| v | Velocidad tangencial | Velocidad tangencial | m/s |
| w | Velocidad angular | Velocidad angular | rad/s |
| a | Aceleración centrípeta | Aceleración dirigida al centro de la circunferencia. | m/s2 |
Respuesta de las demostraciones:
1)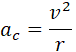 |
2) |
3) |
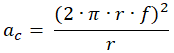
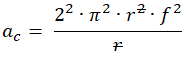
![]()
2) Sabiendo que la circunferencia de un círculo es ![]() , y que la rapidez en el MRU es
, y que la rapidez en el MRU es ![]() demuestre que la siguiente ecuación es correcta:
demuestre que la siguiente ecuación es correcta:
![]()
Solución:
![]()
| Frecuencia (3 fórmulas) | |||||
| Período (3) | |||||
| Velocidad Tangencial (4) | |||||
| Velocidad Angular (2) | |||||
| Radio (5) | |||||
| Aceleración centrípeta (2) |
Es basándose en este tipo de cálculos cómo se hace posible conocer la velocidad de los satélites alrededor de la Tierra (usando fórmulas que veremos en otro tema), todos los técnicos que trabajen con piezas giratorias (CDs, discos, ruedas, piñones, poleas…) tienen que usar conocimientos de MCU para su trabajo.
Continuación de la Práctica de MCU que inició anteriormente.
5) Un cuerpo gira recorriendo 15 rad cada minuto, ¿Cuál es su frecuencia en Hz?
6) La velocidad angular de un cuerpo es 15 rad/s; entonces, da la siguiente cantidad de vueltas por segundo.
Respuesta corta) Complete las siguientes frases con los datos que faltan, y escriba en el respectivo espacio delineado.
7) Un día Pepito amarró unas llaves a un hilo; entonces las hizo girar en MCU recorriendo 14 rad/s, y no se quedó así, también Pepito midió su velocidad obteniendo que es de 3 m/s. Claro, Pepito era un cerebrazo… de modo que por último calculó el radio que describe la circunferencia formada por la chicharra al girar, obteniendo el siguiente resultado _____________
8) La velocidad angular según el SI se mide con la siguiente unidad _____________
9) La aceleración centrípeta según el SI, se mide con la siguiente unidad _____________
10) El periodo según el SI se mide con la siguiente unidad _____________
11) Si un cuerpo en movimiento circular no cambia de magnitud la velocidad,
su movimiento se denomina _____________
12) Una llanta de una bicicleta de 0,5m de diámetro da 40 vueltas en un
minuto, la velocidad de una hormiga en la periferia de la llanta es la siguiente ____________
13) Un cuerpo gira recorriendo 7 rad cada 30s la velocidad angular es la siguiente _____________
14) Un punto sobre un círculo de radio 0,3m gira, viaja a 15 m/s, la aceleración centrípeta del cuerpo es la siguiente ______________
15) Una partícula tiene una velocidad angular de 15 rad/s, el radio que describe es 0.2m, la aceleración centrípeta es la siguiente _____________
16) Un aro de 0,2 m de diámetro gira recorriendo 15 rad en 6s , la velocidad de un punto situado en su periferia es la siguiente _____________
17) Una partícula que gira a 15 m/s dura 12 s en dar una vuelta completa, el radio que describe es el siguiente _____________
Respuestas:
5) Piden frecuencia, pero no se tiene el período:
f = 1 = 1 = 0,039 Hz
T 25,12 s éste dato se calcula abajo…
Buscamos el período pero no se tiene la w:
![]() = 6,28 = 25,12 s
= 6,28 = 25,12 s
Entonces se inicia buscando la w:
Este dato de 15 rad cada minuto no es la w que necesitamos, por eso trabajaremos este dato para obtener una velocidad angular, como se mide en radianes / segundo y tengo radianes / minuto, efectuemos una regla de tres.
15 rad x rad = 0,25 rad/s así obtuvimos w
60s 1 Segundo
6) Lo primero es deducir que lo que le preguntan es frecuencia (cantidad de vueltas por segundo), por eso
f = 1 = 1 = 2,43Hz
T 0,4 s
![]() = 6,28 = 0,41 s
= 6,28 = 0,41 s
15 rad/s
7) 0,2 m 8) rad/s 9) m/s2 10) Segundos 11)MCU 12) 1,03 m/s 13) 0,23 rad/s 14) 750 m/s2 15) 45 m/s2 16) 0,25 17) 28,6 m
La siguiente práctica es más compleja, y requiere que primero comprendas proporcionalidades y el “método de números pequeños” ahí explicado.
Recuerda, Demostraciones fue explicado aquí:
https://www.fisicalinda.com/lessons/demostraciones/#d1
Y proporcionalidades es explicado aquí:
https://www.fisicalinda.com/lessons/proporcionalidades/#p1
Nota: Todos los problemas de proporcionalidad se pueden resolver por demostración también y casi todos los de demostración se pueden resolver por el método de “números pequeños” explicado en el tema de proporcionalidades, así es que ahora disponen de dos herramientas poderosas.
Se sugiere al docente que solicite la respuesta por demostración y por “números pequeños”
1) En una hélice de un avión:
2) Dos discos giratorios de igual radio se mueven con un movimiento circular uniforme. Un punto en el borde del disco I se mueve con una velocidad de magnitud v y el disco II con 2v. En ese punto del borde de cada disco, la magnitud de la aceleración centrípeta del disco I, comparada con la del II es,
| a) la mitad | b) el doble | c) el cuádruplo | d) la cuarta parte |
3) En el carrusel “rueda de caballitos” hay dos niños de igual masa. El niño 1 está montado en el caballito más externo al eje de giro y el niño 2 está montado en un caballito interno. Ambos realizan un movimiento circular de diferente radio, pero con igual período de revolución; entonces es correcto afirmar:
| a) | la aceleración centrípeta del niño1 es menor que la del 2 y de direcciones opuestas. | |
| b) | la velocidad tangencial del niño 1 es mayor que la del 2, pero de igual dirección. | |
| c) | la fuerza centrípeta sobre ambos niños tiene igual magnitud y dirección. | |
| d) | el niño 1 da más revoluciones por unidad de tiempo que el niño 2. | |
RESPUESTAS
1 a)
| Solución por demostración. | Solución por números pequeños |
| Escribo un supuesto: las partículas “b” (cerca del eje) están a r y las”a” están a 2r.
Busque la(s) fórmula(s) que se aplica(n) al caso de acuerdo con los datos.
Despeje una variable que NO le den en el ítem y sea igual en ambos casos. Se puede despejar T o pi, pero es más fácil el procedimiento con pi. Elabore una igualdad sustituyendo con las variables del ítem. Note que las partículas “a” están más lejos, por eso escribo 2.r Necesita averiguar la velocidad, por ejemplo, de las partículas a:
Conclusión: las partículas “a” viajan más rápido. |
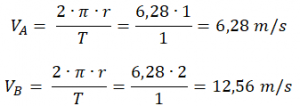
Conclusión : Las partóculas cercanas al eje « b » viajan más rápido.
|
1b) ¿Cuáles partículas (a, b) tienen más velocidad angular?
| Solución por demostración. | Solución por números pequeños |
| Escribo un supuesto: las partículas “b” (cerca del eje) están a r y las”a” están a 2r.
Busque la(s) fórmula(s) que se aplica(n) al caso de acuerdo con los datos.
Despeje una variable que NO le den en el ítem y sea igual en ambos casos. Despejaremos v porque ocupo
Elabore una igualdad sustituyendo con las variables del ítem. Esta igualdad no es válida porque eso es decir:
Velocidad tangencial de partículas “a” es igual a velocidad tangencial de partículas “b” y eso no es cierto. Si continúas vas a llegar a un resultado que no es coherente con la realidad:
Conclusión: Por demostración usando esa fórmula no se llega al resultado, al inspeccionar la otra fórmula:
Se deduce que la velocidad angular nunca cambia. |
Para las partículas “a”, le asignamos un radio de 2, pero del resultado del ítem anterior descubrimos que si usamos radio 2.r, la velocidad aumenta a 2.V, entonces:
Conclusión: Tienen igual velocidad angular. |
1c) Las partículas B. 2) d 3) b
Indicador: Aplica los conocimientos de MCU en la resolución de una práctica de MCU.
Proceso: Presenta los procedimientos para resolver satisfactoriamente los ejercicios propuestos seguidamente.
Evaluación: 5pt fórmulas correctas, 5pt procedimientos correctos, 5 pt resultados correctos, 5pt uso de magnitudes correctas. Total 20 pt = ____%
Fecha de entrega:_________
Nota al alumno: Si usas una calculadora Casio moderna (programable) y puedes programarla en shift + mode 72 (Fix con dos decimales), hazlo, te ayudará al redondearte los resulta dos automáticamente, presiona la tecla Shift+Mode + la tecla 7 y la tecla 2, en ese orden.
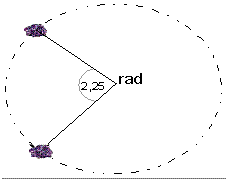
1) Una piedra atada a un hilo y gira con M. C. U si describe un ángulo de 2, 25 rad en 0, 2 s y el radio de la circunferencia es 40cm. Calcule:
2) Un disco efectúa 120 revoluciones por minuto (r.p.m) con MCU. Calcule:
3) Un cuerpo describe un círculo de radio 50cm con MCU. El cuerpo de 30 vueltas por minuto. Calcule su aceleración centrípeta
4) ¿Cuál es la velocidad angular de rotación de la Tierra si el radio de la Tierra es 6,37×106m? También calcule la velocidad de un punto en el ecuador.
5) Calcule la velocidad Angular y lineal de la Tierra, sabiendo que da una vuelta completa alrededor del Sol cada año y su distancia promedio al Sol es 1,49×108 km.
1a) 11,25 rad/s. 1b) 4,50 m/s. 1c) 0,56 s 1d) 1,79 revoluciones/s o Hz.
2a) 0,5 s 2b) 2 Hz 2c) 12,56 rad/s 2d) 37,68 m/s.
3) 4,9m/s2 4) w = 7,26x 10-5 rad/s , v=462 m/s 5) w = 1.99x 10-7 rad/s , v= 29,6 km/s
Regresa al experimento que hiciste al principio del tema:
1) Si la circunferencia de un círculo se mide con 2¶ r. Y tienen que calcular la velocidad con que giran las llaves qué fórmula construirían y por qué? Hagan el cálculo y verifiquen que obtengan un resultado lógico. Recuerde que en MRU la velocidad era v= d/t.
2) Sabiendo que un círculo tiene 2¶ radianes (radianes es otra forma de medir ángulos, esto es como decir que un círculo tiene 360°), y que llamamos velocidad angular a la velocidad con que la partícula recorre esos 2¶, ¿Cuál fórmula construiría para calcular la velocidad angular?
¡Pruébela para ver si funciona!.