Fuerzas en X y en Y

El vídeo anterior debe ser visto en su totalidad para que se le consigne progreso en el curso

Fuerzas en “X” y en “Y”

Vamos a ampliar el concepto de Fuerza, para ello ahora trate de alzar su mesa en un ángulo de 30° respecto a la horizontal, luego hágalo en un ángulo de 90°

¿Puede notar que a los 30° tiene que hacer mucha más fuerza para alzarla que la que usa a los 90°? ¿Sabe por qué?. Es por qué el ángulo de aplicación de la fuerza disminuye el valor de la componente de la fuerza en el eje Y; pero, para entender estos términos debes estudiar lo que sigue, por ello ahí le vamos.

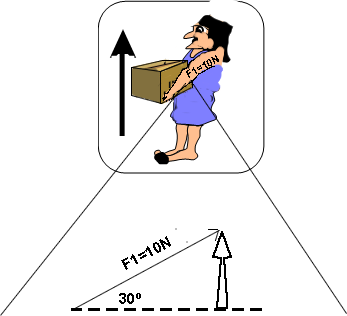
En realidad la fuerza de nuestro brazo se puede interpretar con el siguiente diagrama

Cuando se aplica una fuerza la puede aplicar en el eje “X”, en el eje “Y”, o entre ambos ejes, como en el ejemplo del hombre que levanta la caja, él hace fuerza en un ángulo de 30°, esta fuerza está entre ambos ejes, esto se puede representar en un eje de coordenadas cartesianas o plano cartesiano, siguiendo el anterior ejemplo:

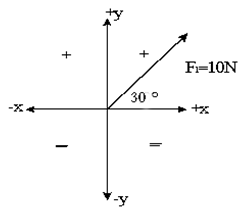
Supongamos que la fuerza (F1) es de 10 N a 30°.     Note que F1 está entre ambos ejes, por esto tiene valor en “x” y valor en “y”.   Cuando debamos averiguar el valor de la fuerza en el eje X (F1x), o en el eje Y (F1y), se debe hacer por trigonometría, como se manifiesta seguidamente para la fuerza F1 :

Aquí ocupas en cateto adyacente al ángulo, ya que

Ya que:   Cat. Adyac = F1x Hipotenusa = 10 N Entonces 30. 10N= 8,66 N

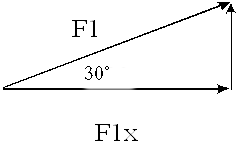Podríamos generalizar que para este caso:

F_1x= cos θ. F₁

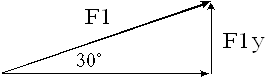
Y en el caso de la fuerza en Y, debido a que es el cateto opuesto al ángulo, entonces usamos la función seno porque:

Ya que: Cat. Opuesto = F1y Hipotenusa = 10 NEntonces 30.10N= 5 N Nuevamente, para este caso podríamos generalizar y decir que: F1y= sen θ. F1

Estos dos resultados significan que si yo aplico 10N de fuerza a 30° halando una mesa, para moverla (en la dirección de X) solo estoy aplicando 8,66N, y hacia arriba (levantarla, en dirección de Y) estoy aplicando 5N.

Antes de iniciar una práctica recuerda la distribución de los ángulos en el círculo trigonométrico.

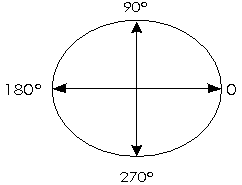Amplia la comprensión explorando este laboratorio virtual:

Práctica:

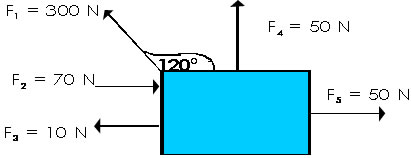
1) Averigüe el valor en el eje “x” y en el eje “y” de las siguientes fuerzas:

2) ¿Cuál es la aceleración de la siguiente caja?

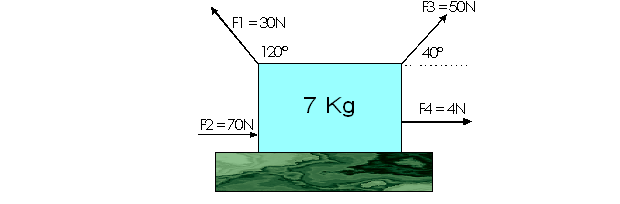
Note que la aceleración se averigua con F_x ¿Por qué no con F_y?, bueno es porque la caja se moverá sobre el piso (eje x); pero, si en algún ejemplo tuviera que calcular la aceleración con que viaja hacia arriba; entonces, si podría usar Fy; pero, en todos los ejemplos que siguen se mueve sobre el piso.

3) Ésta es una caja con un televisor, la caja está amarrada a la pared con una cuerda (representa F1) y hay dos niños tratando de llevarse la caja, uno la hala (F2) el otro la empuja (F3), ¿logran los niños llevarse la caja? ¿Con qué aceleración la arrastran y hacia dónde?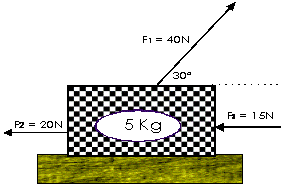

4) ¿Cuál es la aceleración en x de esta caja y hacia donde en x se mueve? Nota: use dos decimales en el resultado.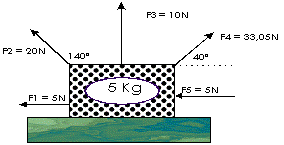

Respuesta:

1)

2)

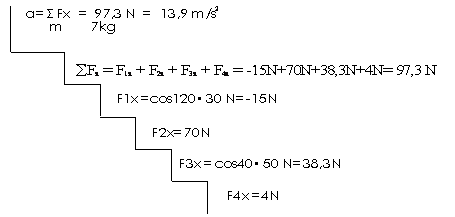
3) Si se la llevan. La aceleración es -0,07m/s² a la izquierda.

4) No se mueve a x = 0

Si terminó, explore este laboratorio virtual, el que dice Net Force y Aceleration;  observe cómo es que se suman o restan fuerzas en X:

Vamos a practicar con los conceptos aprendidos, el primer problema está resuelto: