Las fuerzas elásticas

¿Qué es un cuerpo elástico? __________________________________

Cite 3 ejemplo de cuerpos elásticos y no elásticos: ______________________

_________________________________________________________________________

 

Seguramente algunos de ustedes dirán que cuerpos elásticos son: el Hulefante, el Resorteronte y la Ligartija, y eso muestra que tienen la noción de elasticidad. Para poner un ejemplo muy ilustrativo, de las siguientes sustancias, una bola de plastilina o una bola de acero, ¿Cuál de ellas es más elástica?, la respuesta quizá le sorprenda, antes de dar la respuesta, definamos elasticidad.

 

                       Elasticidad se define como “la resistencia de un cuerpo a ser deformado permanentemente”, por ello en el caso de las dos bolas, la más elástica es la de acero, porque es más difícil deformarla. Hay fuerzas denominadas elásticas, las cuales son las fuerzas de reacción de algunas sustancias elásticas que responden en contra de la deformación, tal como son los materiales de los cuales se hacen los resortes, si usted trata de deformar un resorte comprimiéndolo o estirándolo, él responde a este cambio impidiendo su deformación (en la medida de lo posible, haciendo una fuerza en sentido contrario, cuyo valor está dado por la Ley de Hooke:

Fe = -k •ΔX

Fe: Fuerza restauradora elástica (se mide en Newtons). En todos los casos es una fuerza de reacción a la fuerza aplicada que deforma la sustancia, si se cuelga algo, la fuerza restauradora elástica será proporcional a la fuerza resultante del peso del cuerpo, si el resorte arrastra algo la fuerza restauradora elástica será proporcional a la fuerza que venza el resorte para arrastrarlo (quizá igual a la fricción).   k: Constante elástica (se mide en N/m). Depende del material, área de la sección y la longitud (del resorte). Note el signo negativo que precede a k, este signo se debe a que la fuerza elástica siempre se opone a la deformación; entonces, se agrega este para obtener una fuerza negativa, cuando el ΔX es positiva. ΔX: Elongación o cambio de longitud del resorte = dfinal – dinicial. Es la cantidad que se estira (se mide en metros).

 

Entonces la fórmula para averiguar la fuerza elástica de un resorte es:

Fe = -k • ΔX= IFeI

Y el signo de menos antes de k (-k), solo es útil para indicar que la fuerza que hace el resorte se opone a la deformación, o sea, si lo estiran él hace fuerza para encogerse; pero, si lo comprimen él hace fuerza para estirarse, siempre contrario a la deformación. Conociendo que este es negativo es sólo con ese propósito, a muchos les ha sido muy útil usar el valor absoluto en la fórmula (sin el signo):                                                

Fe= k•ΔX

A nivel de estudiantes de cuarto año, es más simple usarla de este modo. En este libro se usará sin el negativo. En este tema estaremos trabajando con un tipo de resortes que se llaman proporcionales, eso significa que se estiran en proporción exacta al peso colgado, por ejm, si con 1kg se estiró 10 cm, con 2kg se estirará 20 cm, con 3 kg se estira 30 cm, etc, por ello también puede resolverlos con reglas de tres.

Para comprender el concepto mejor veamos unas demostraciones, en esta primera, por favor elija la que se llama “intro”:

En este otro laboratorio elija también la opción que dice “intro”:

Finalmente analice el siguiente dibujo:

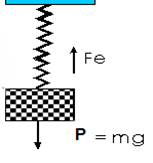
¿Puede notar que la Fuerza elástica Fe es exactamente igual al peso de la carga?

Entonces llegamos a dos nuevas fórmulas:

Fe = P

K .ΔX = m.g            Preste mucha atención a ésta fórmula porque es muy útil para este tema.

Práctica:

Resolución de problemas: Responda correctamente lo que se le solicita.

Elabore análisis dimensional de la fórmula aplicada y las conversiones de cm a m.

Nota: es importante que sepas hacer análisis dimensionales, puedes repasarlo aquí:

https://www.fisicalinda.com/lessons/analisis-dimensional/#fe

Y conversiones:

https://www.fisicalinda.com/lessons/conversiones/

 

1) Si a un resorte proporcional le colgamos una masa de 2kg se estira 20cm, calcule: los siguientes aspectos.

 

• a) Averigüe la Constante elástica. 1pt fórmula correcta, 2pt sustitución (valores y unidades) correcta, 1pt resultado correcto. Total: 4pt. Note que se le da el puntaje, es para que se vaya familiarizando con la forma de evaluar, de modo que mientras trabaja se prepara para prueba.

 

 

 

• b) Usando el mismo problema ahora calcule la fuerza elástica que hace ese resorte. 4pt

 

 

 

• c) Usando el mismo problema ahora ¿Cuánto se estira si ahora cuelgo 1kg? 4pt

 

 

 

 

• d) Usando el mismo problema ahora ¿Cuál es la masa del cuerpo colgado si el resorte se estira 10cm? 4pt

 

 

 

2) Cuando le colgamos 1 kg a un resorte (que es proporcional o lineal), éste se estira 10 cm.

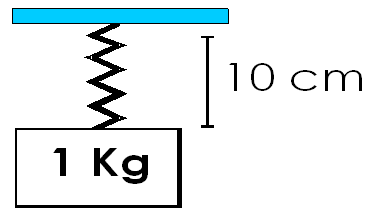Calcule:

• a) Constante elástica del resorte. 4pt

 

 

• b) Si el piso está a 0,3m, ¿llega al piso cuando se le cuelgan 2 kg de masa al resorte? 4pt

 

 

 

• c) ¿Cuánta masa tiene que colgársele al resorte para que se estire 5cm? 4pt

 

 

 

3) Tenemos una bolsa colgada de un resorte proporcional, si la bolsa pesa 60N y se ha estirado medio metro, averigüe lo siguiente

• a) La masa colgada. 4pt

 

 

 

 

• b) La constante elástica. 4pt

 

 

 

 

• c) Si en otra ocasión este mismo resorte se estira 10 cm ¿cuál es la masa colgada? 4pt

 

 

 

4) Con un cuerpo de 5N un resorte proporcional se estira 25cm, calcule:

 

 

• a) La masa colgada4pt .

 

 

 

• b) La fuerza que hace el resorte. 4pt

 

 

 

• c) ¿Cuál es la masa si este mismo resorte se estira 50 cm? 4pt

 

 

 

5) Un resorte proporcional cambia su longitud de 20cm a 35cm cuando se le cuelga un cuerpo de 1,5kg calcule:

• a) La fuerza elástica. 4pt

 

 

 

 

 

• b) ¿Cuánto se estira este mismo resorte con 2kg? 4pt

 

 

 

• c) ¿Cuál es la masa si este mismo resorte se estira 50 cm? 4pt

 

 

Profundización

Resuelva los siguientes problemas, que requieren un poco más de pericia.

6) Una caja de 2kg es arrastrada horizontalmente por un resorte cuya constante es k = 200N/m sujeto a la pared; si entre el piso y la caja hay una fuerza de fricción con μk = 0,3 y la caja se desplazó 0,8m, cuál aceleración experimentó la caja. 3pt calculo fricción, 5 pt cálculo aceleración. 8pt.

 

 

 

 

 

 

7) Una caja que pesa 15N es arrastrada por un resorte con k= 300N/m sujeto a la pared; si entre el piso y la caja hay una fuerza de fricción con μk = 0,07 y la caja se mueve 0,5m. ¿Cuál aceleración experimentó la caja? 3pt calculo fricción, 5 pt cálculo aceleración. 7pt.

 

 

 

 

8) Una caja que pesa 18N es arrastrada por un resorte con k= 500N/m sujeto a la pared; si entre el piso y la caja hay una fuerza de fricción con μk = 0,25 y la caja originalmente estaba a 2m de la pared y después se mueve hasta estar a 1,5m de la pared ¿cuál aceleración experimentó la caja? 3pt calculo fricción, 5 pt cálculo aceleración. 8pt.

 

 

 

 

9) Observe el siguiente video del pobre Coyote:

Si la constante elástica de ese resorte es de 300 N/m y se estira 7 m ¿cuánta fuerza hace Coyote sosteniéndose de la roca?

 

 

Respuestas:

 

1)      a) Averigüe la Constante elástica.   R/ Procesos para resolverlo: Datos: m= 2kg    ΔX= 20 cm = 0,2 m     k=?   Formula: K .ΔX = m.g Despejo K K= m.g =  2kg . 9,8m/s2 = 98 N/m ΔX               0,2 m El análisis dimensional sería este: A.D K= m.g ΔX Ahora sustituyo todo por unidades N/m = kg . m/s2 m Ahora observe que kgm/s2 es igual a Newton, entonces solo sustituyo arriba por N y listo N/m = N             m b) Usando el mismo problema ahora calcule la fuerza elástica que hace ese resorte Respuesta. Recuerde que una vez calculada k para un resorte, es la misma siempre, en toda situación. Pero, OJO, cada resorte o cuerpo tiene k diferente. Necesito Fuerza elástica y como Fe = k • ΔX = 98 N/m (0,2m – 0) = 19,6 N Note que el valor de esta fuerza es igual al peso del cuerpo colgado ¿Por qué?  Por supuesto, el resorte reacciona con igual fuerza que la carga, en este caso la fuerza ejercida por el peso del cuerpo Fe = Fa = mg. c)   Usando el mismo problema ahora ¿Cuánto se estira si ahora cuelgo 1kg? Respuesta. a) Como la fuerza aplicada es igual en magnitud al peso Fe = P = m•g = 1 kg • 9,8 m/s2 = 9,8 N b) Necesito ΔX; entonces, lo despejo de la fórmula Fe = k •ΔX y obtenga ΔX = Fe =   m•g =   9,8N    =  0,1m k         k        98N/m d) Usando el mismo problema ahora ¿Cuál es la masa del cuerpo colgado si el resorte se estira 10cm? Respuesta. d. a) Para calcular esta masa debo saber que el resorte se estirará por acción del peso de la masa colgada, P = m.g de donde despejo masa y obtengo m =  P         g d. b) Pero la fuerza que hace el resorte es equivalente a la fuerza resultante del efecto del peso de la masa, de modo que Fe = Fa = P   y si Fe = k . ΔX = 98 N/m . 0,1 m = 9,8 N Entonces sustituyo en la fórmula de masa m= P  =      Fe         =      9,8N      =  1kg g        9,8m/s2           9,8 m/s2

Respuestas del resto de problemas:

2) a) 98 N/m,   b) No, pues se estiró 0,2 m,   c) 0,5 kg   3)    a) 6,12 kg,     b)120 N/m,    c) 1,24 kg 4)    a)0,51 kg,      b)5N,              c)1,02 kg

5)    a)14,7N,        b) 0,2 m,         c) 5 kg   6)77,06 m/s2 7)97,35 m/s2 8)134,15 m/s2

 

 

Experimento de profundización. Fuerzas elásticas

Objetivo específico: Aplica los conceptos de fuerza elástica que aprendió.

Ahora regrese a los datos obtenidos en el experimento de focalización al inicio del tema, si no lo hizo por alguna razón, ahora es momento de realizarlo.

Usando la información de la tabla de datos o del gráfico, calcule la constante elástica de ese resorte y ahora:

• Calcule cuánto se estira con 4 monedas.

 

 

 

• Su resultado es coherente con los resultados del experimento, de no ser coherentes ¿qué errores pueden existir?