Ley de Coulomb y Campo eléctrico
Ley de Coulomb.
Coulomb hizo un experimento interesante colocando una pequeña partícula cargada en una manilla que la sostenía, cuando se acercó una carga opuesta y la partícula fue atraída, de modo que le permitió calcular el valor de la fuerza, entonces Coulomb propuso su famosa ley:
“La fuerza de atracción o repulsión entre dos cargas puntuales (cuerpos cargados cuyas dimensiones son despreciables comparadas con la distancia r que las separa) es inversamente proporcional al cuadrado de la distancia que las separa”.
En el siguiente link usted podrá ver los detalles de un experimento virtual que permite llegar a la Ley de Coulomb.
http://www.thephysicsaviary.com/Physics/Programs/Labs/CoulombsLawLab/index.html
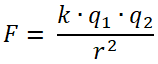 |
k= es un valor constante de 9×109 Nm2/C2.
q1 y q2= son los valores en Coulombs de las dos cargas. r= distancia de separación entre las cargas, se mide en metros. |
La siguiente aplicación ayudará al docente a explicar el concepto de proporcionalidad, tan importante en física.
Recuerda de tu caja de herramientas el tema de proporcionalidades: https://www.fisicalinda.com/lessons/proporcionalidades/
El siguiente link es recomendado para que el estudiante perciba la relación de proporcionalidad que existe entre las variables en la Ley de Coulomb.
http://www.thephysicsaviary.com/Physics/Programs/Labs/ForceElectricMiniLab/index.html
Práctica:
1) Dos cargas q1 = 5,4 x 10-14 C y q2 = 7,3 x 10-10 C, están separadas por una distancia de 9,0 x 10-5 m; Calcule la magnitud de la fuerza electrostática de repulsión entre ellas.
R/ 4,38×10-5N.
Campo eléctrico
Fue entre los siglos XVI y XVIII cuando se da una verdadera revolución iniciada quizá por Volta quien trabajó arduamente en la elaboración de pilas eléctricas, las cuales Ampere y Faraday usaron para hacer experimentos demostrativos, que les permiten exponer los efectos de la electricidad en los seres vivos y en diferentes materiales.
A la zona del espacio donde se perciben los efectos de una Fuerza de origen eléctrico, se le denomina “Campo eléctrico” y se mide en N/C (Newtons / Coulombio), el campo eléctrico se extiende teóricamente hasta el infinito.
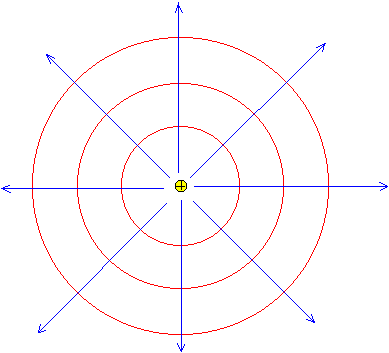
El campo eléctrico alrededor de una carga puntual se puede representar como esferas concéntricas alrededor de la partícula y esta dado por:
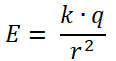
k= es un valor constante de 9×109 Nm2/C2.
E= campo eléctrico, se mide en N/C.
q= Valor en C de la carga eléctrica.
r= distancia en metros de separación hasta donde se mide el campo.
Por convención se acepta que el campo eléctrico sale del positivo y va hacia el negativo tal como se muestra en la imagen.
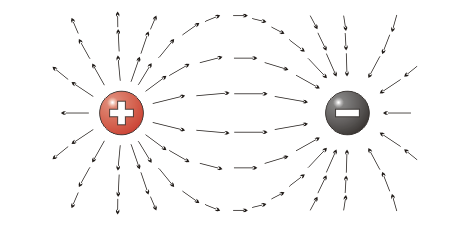
Otra forma de escribir la misma fórmula anterior involucra la idea de que el campo eléctrico origina una fuerza eléctrica, dada por F = q.E
Si relacionamos esta fórmula de fuerza con la de campo, obtenemos:
E= F/q
E= Campo eléctrico, se mide en N/C.
F= Fuerza producida por el campo eléctrico, se mide en N.
q= Una carga de prueba sometida a la acción del campo, su valor es dado en Coulombios (C).
Vamos a obtener una nueva fórmula para averiguar el trabajo de una carga electrostática.
Sabiendo que W= F.d y que F = q.E obtenga una nueva fórmula de trabajo que pueda ser usada para cargas electrostáticas:

Respuesta:
Si el campo es uniforme, tal como el campo creado por dos placas paralelas cargadas. El trabajo para desplazar la carga será igual al producto de la fuerza (F= q.E) constante por la distancia que se desplaza en la dirección de la fuerza.
De modo que
W = q.E.d W= Trabajo, se mide en Julios (J).
q= Una carga de prueba sometida a la acción del campo, su valor es dado en Culombios (C).
E= Campo eléctrico, se mide en N/C.
d= Distancia recorrida, se mide en m.
Nota: El trabajo para mover una carga de un punto a otro es una cantidad vectorial.
| Posteriormente Michael Faraday (1791- 1867) hace un experimento en el cual enrolla un cable por el que circula una corriente, dentro de la bobina formada (cable enrollado) puso otra bobina con un galvanómetro (medidor de corriente) conectado a ella y notó que cuando circulaba corriente en la primer bobina, aparecía una corriente en la segunda bobina, debido a un pequeño cambio en el campo magnético que se generaba, esto le hizo concluir que las corrientes eléctricas inducen campos magnéticos y éstos pueden nuevamente inducir corrientes eléctricas en una segunda bobina.
|
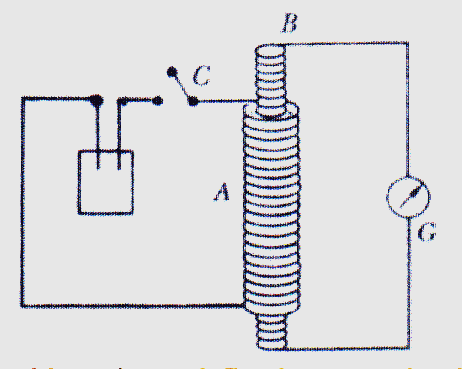 |
Potencial eléctrico y Aplicaciones
Cuando la carga eléctrica se mueve, cambia de energía potencial y a “la energía potencial por unidad de carga se le denomina Potencial Eléctrico”, o simplemente Potencial y se representa con V y su valor en cualquier punto de un campo eléctrico se mide por el trabajo que debe efectuarse sobre la unidad positiva de carga a fin de moverla a velocidad constante desde una distancia infinita hasta el punto en cuestión.
O sea:
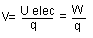
V= Potencial o Voltaje, se mide en Voltios (V) = Julios/Coulomb (J/C).
Uelect= Energía Potencial Eléctrica, se mide en Julios (J).
W= trabajo, se mide en Julios (J).
q= Carga eléctrica de prueba, se mide en Coulombs (C).
Ello significa que la diferencia de potencial (o voltaje) entre dos puntos a, b, es igual al trabajo necesario para mover una carga eléctrica desde a hasta b.
El generador de Van de Graaff.
Si recordamos, al frotar algunas sustancias, se cargan eléctricamente, ese es el principio que usó Van de Graaff en 1931 para construir una máquina que permitía establecer una diferencia de cargas de hasta 20 millones de voltios que luego era descargada en un objetivo puntual.
El generador de Van de Graaff es muy simple, consta de un motor, dos poleas, una correa o cinta, dos peines o terminales hechos de finos hilos de cobre y una esfera hueca donde se acumula la carga transportada por la cinta.
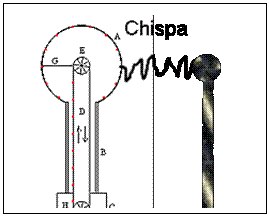
En la figura, se muestra un esquema del generador de Van de Graaff. Un conductor metálico hueco A de forma aproximadamente esférica, está sostenido por soportes aislantes de plástico, atornillados en un pie metálico C conectado a tierra. Una correa o cinta de goma (no conductora) D se mueve entre dos poleas E y F. La polea F se acciona mediante un motor eléctrico.
Dos peines G y H están hechos de hilos conductores muy finos, están situados a la altura del eje de las poleas. Las puntas de los peines están muy próximas, pero no tocan a la cinta.
La rama izquierda de la cinta transportadora se mueve hacia arriba, transporta un flujo continuo de carga positiva hacia el conductor hueco A. Al llegar a G y debido a la propiedad de las puntas se crea un campo lo suficientemente intenso para ionizar el aire situado entre la punta G y la cinta. El aire ionizado proporciona el medio para que la carga pase de la cinta a la punta G y a continuación, al conductor hueco A, debido a la propiedad de las cargas que se introducen en el interior de un conductor hueco.
El generador de Van de Graaff ha sido usado para estudiar campos eléctricos de alta magnitud.
Práctica:
- 1) Una carga eléctrica de 3,5 x 10-7 C, produce un campo eléctrico de 1,5 x 106 N/C, a una distancia de
| a) 4,6 x 10-2 m | b) 2,1 x 10-3 m | c) 4,8 x 10-7 m | d) 2,3 x 10-13 m | R/ a |
- 2) Toda carga eléctrica tiene asociado un campo eléctrico a su alrededor. Una carga eléctrica de +8,0 x 10-10 C, produce a una distancia de 0,40 m, un campo eléctrico de
| a) | 45 N/C, hacia la carga | |
| b) | 18 N/C, hacia la carga | |
| c) | 45 N/C, alejándose de la carga | |
| d) | 18 N/C, alejándose de la carga | R/ c |
- 3) Una carga de magnitud 1,8 x 10-10 C, produce un campo eléctrico de intensidad 18 N/C, a una distancia de la carga igual a
| a) 11 m | b) 3,3 m | c) 0,30 m | d) 0,090 m | R/ c |
- 4) De acuerdo con la figura, la intensidad del campo eléctrico que genera un protón en un punto P1 es
1,31 x 10-19 N/C, y en el punto P2 es E2.
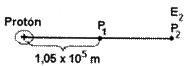
Si la distancia del protón a P1 es igual a la distancia de P1 a P2 y el protón tiene una carga eléctrica de 1,6 x 10-19 C, entonces, ¿cuál es el valor de E2?
| a) 1,6 x 10-20 N/C | b) 3,3 x 10-20 N/C | c) 6,6 x 10-20 N/C | d) 2,6 x 10-19 N/C | R/ b |
- 5) Una partícula alfa tiene la carga eléctrica de dos protones, es decir, 3,20 x 10-19 C una distancia de 5,00 x 10-10 m de dicha carga, la magnitud y dirección del campo eléctrico que genera es
| a) | 5,76 N/C, hacia la partícula | |
| b) | 1,15 x 1010 N/C, hacia la partícula | |
| c) | 5,76 N/C, alejándose de la partícula | |
| d) | 1,15 x 1010 N/C, alejándose de la partícula | R/ d |
- 6) Una partícula de carga q genera un campo eléctrico de intensidad E en un punto que está a la distancia 4,0 x 10-8 m de ella. Si se remplaza la partícula por otra de carga 4q, se producirá en otro punto un campo de igual intensidad E, cuando la nueva partícula esté a una distancia de ese punto, igual a
| a) 1,6 x 10-7 m | b) 1,0 x 10-8 m | c) 2,0 x 10-8 m | d) 8,0 x 10-8 m | R/ d |
Solución:
La clave para resolverlo está en que dice: “se producirá en otro punto un campo de igual intensidad E”, eso me indica que tengo que hacer una igualdad, en palabras simples, hay una condición inicial y una final que son iguales en el campo eléctrico, ya que
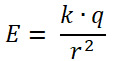
entonces debo comparar el campo inicial y el final para averiguar la distancia a que se forma con la segunda carga, lo haré así: Einicial = Efinal
Solución:
La clave para resolverlo está en que dice: “se producirá en otro punto un campo de igual intensidad E”, eso me indica que tengo que hacer una igualdad, en palabras simples, hay una condición inicial y una final que son iguales en el campo eléctrico, ya que
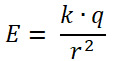
entonces debo comparar el campo inicial y el final para averiguar la distancia a que se forma con la segunda carga, lo haré así: Einicial = Efinal

- 7) Un electrón (q= 1,6×10-19 C) en reposo produce un campo eléctrico de intensidad 5,4 x 105 N/C, a una distancia, respecto de él, de
| a) 1,3 x 102 m | b) 5,2 x 10-8 m | c) 2,7 x 10-15 m | d) 5,4 x 10-13 m | R/ b |
- 8) ¿Cuál es la intensidad del campo eléctrico que produce una carga puntual de 1,6 x 10-18 C a 1,5 x 10-6 m de ella?
| a) 1,1 x 10-12 N/C | b) 7,1 x 10-7 N/C | c) 9,6 x 10-3 N/C | d) 6,4 x 103 N/C | R/ d |
9) ¿Cuál es la distancia de separación entre dos electrones (1,6×10-19 C) que se repelen con una fuerza electrostática de magnitud 5,00 x 1012 N?
- 6,79 x 10 -9 m
- 4,61 x10 -17 m
- 7,16x 10 -14 m
- 3,47 x 10 -3 m
- 10) La fuerza electrostática entre q1 y q2 es de 1,2 x 10-11 Si q1 es igual a 9,9 x 10-12 C y está separada de q2 una distancia de
5,0 x 10-5 m, el valor de q2 es
- 4,3 x 10-10 C
- 3,4 x 10-19 C
- 6,7 x 10-12 C
- 5,3 x 10-30 C
- 11) Dos partículas de igual carga eléctrica y separadas por una distancia de 0,10 m, se repelen con una fuerza electrostática de magnitud 5,1 x 1011 Si ambas son de carga positiva, ¿cuál es la carga de cada una?
- 0,75 C
- 0,57 C
- 0,28 C
- 1,3 C
12) Se tienen dos cargas iguales de q cada una, separadas una distancia d, y la fuerza electrostática entre ellas es de magnitud F. Si una de las cargas se mantiene constante, la otra se hace variar hasta (4/9)q y la distancia de separación se mantiene constante, entonces, comparada con F, ¿cómo debe ser la magnitud de la nueva fuerza electrostática?
- (16/81) F
- (2/3) F
- (4/9) F
- (9/4) F
Práctica para examen de Ley de Coulomb:
La siguiente práctica solo se hará visible para usuarios registrados cuando usted haya visto en su totalidad el vídeo al inicio de esta lección.
