Proporcionalidades
Aprender a interpretar situaciones en términos de la proporcionalidad exstinte entre sus variables, es una habilidad indispensable en física, por eso este es otro tema importante para que esté en tu “caja de herramientas” de física.
Seguidamente se explican proporcionalidades en algunos temas, pero los principios que aprendas, son aplicables para todo tema de física.
Vídeo que explica proporcionalidades, minuto 24,50 en adelante:
Proporcionalidades en le tema Movimiento Circular Uniforme.
Cuando hablamos de proporcionalidades, nos referimos a la forma como dos valores o variables (distancia con tiempo, velocidad con aceleración y otros) se relacionan entre sí, y tenemos dos tipos:
- A) PROPORCIÓN DIRECTA: Esta es cuando al aumentar el valor por multiplicación por un número de una variable aumenta igualmente el resultado obtenido (o sea aumenta la otra variable), por ejemplo:
En la fórmula![]()
La velocidad es “directamente proporcional” al radio.
Esto se debe a que al aumentar el valor del radio aumenta el resultado de la velocidad.
Probémoslo; usemos números inventados y pequeños por facilidad, en el caso A utilicemos un radio de 1y en el caso B un radio de 2.
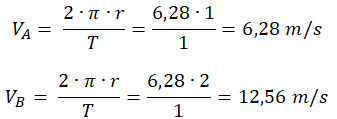
Como ves, al aumentar el radio al doble, aumenta la velocidad al doble, por eso se dice que hay una proporción directa entre ellos.
Una proporción directa también se puede apreciar en la relación que existe entre las variables de una gráfica, por ejemplo:
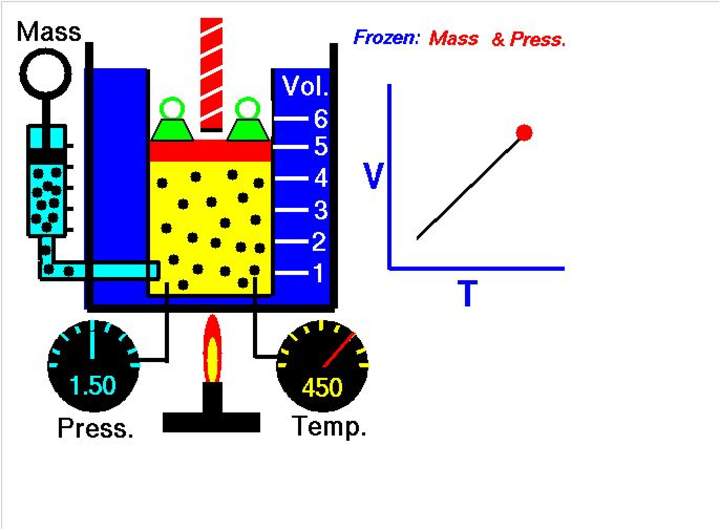
Esto muestra la proporción directa entre la temperatura y el volumen cuando no variamos la presión. Entonces la presión aumenta directamente al aumentar la temperatura y a la inversa:
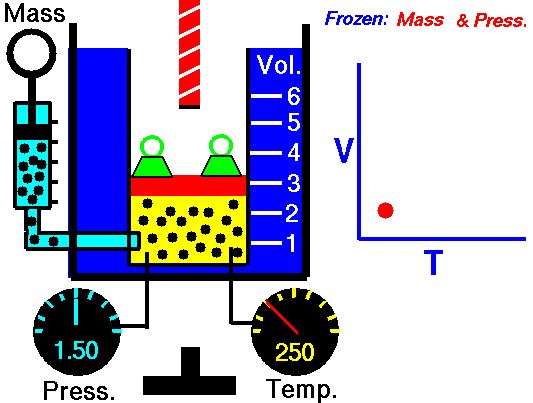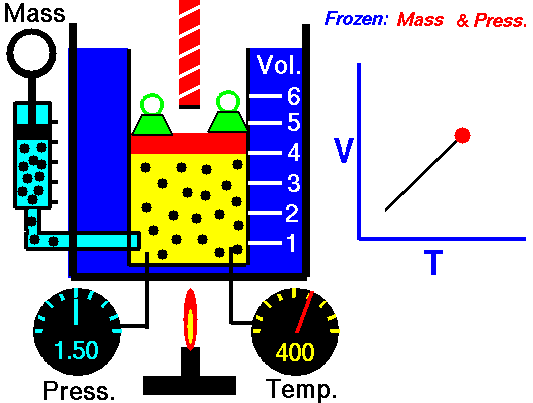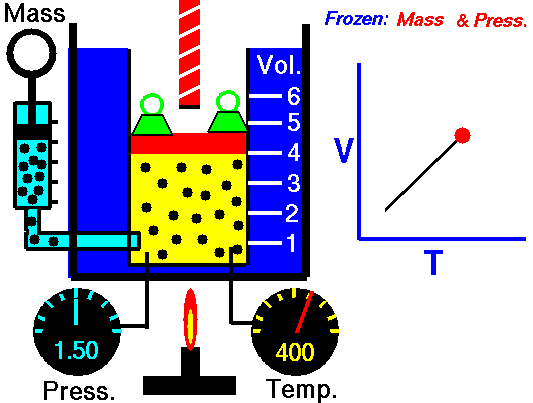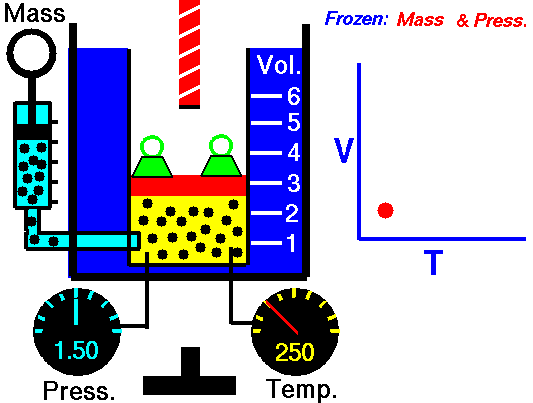
Tomado de: https://www.curriculumnacional.cl
- B) PROPORCIÓN INVERSA: Cuando al aumentar el valor de una variable por multiplicación por un número, disminuye el resultado por división por el mismo número, se dice que hay “proporción inversa” entre ellas, por ejemplo:
En la formula ![]()
La velocidad es “inversamente proporcional” al periodo.
Esto se debe a que al aumentar el valor del periodo, disminuye el resultado de la velocidad, probémoslo, usemos números inventados y pequeños por facilidad, en el caso A utilicemos un período de 1s y en el caso B un período de 2s.
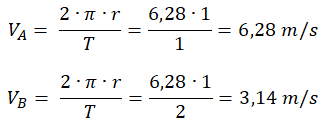
Como ves, al aumentar el período dos veces, la velocidad disminuye a la mitad, por eso se dice que hay una proporción inversa entre ellos.
Como un ejemplo de cómo ha relación inversa entre variables de una gráfica, podemos estudiar la relación entre el Volumen y la presión en un proceso isotérmico (sin cambio de temperatura). El aumento de volumen hace que directamente proporcionalmente aumente la presión como se ven en las siguientes dos imágenes:
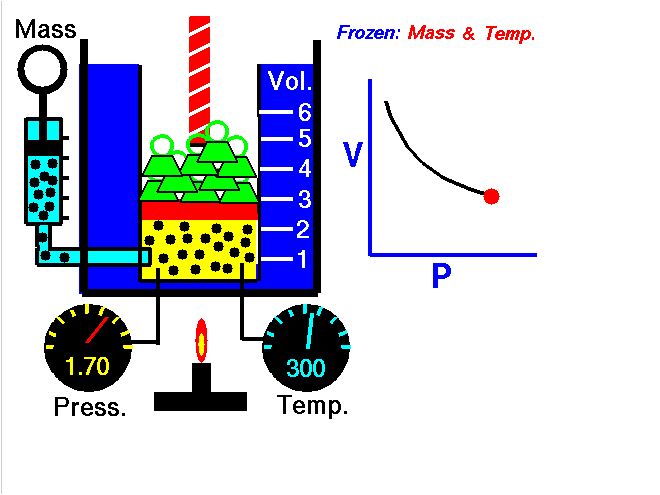
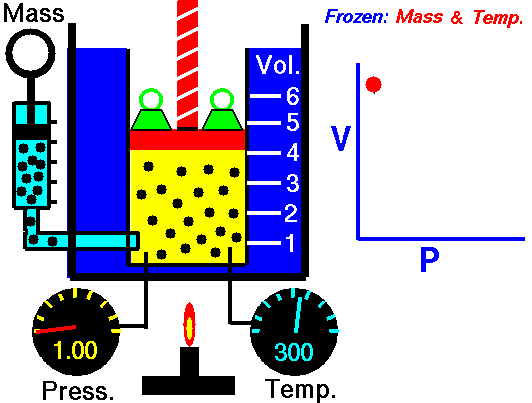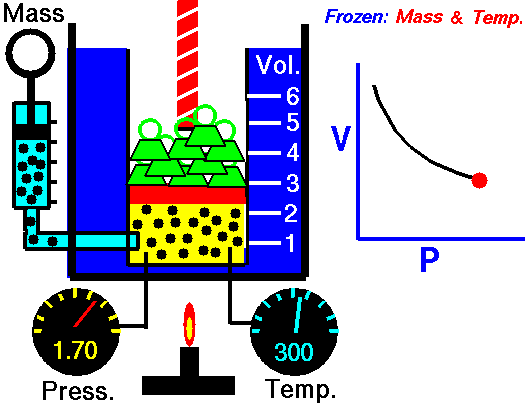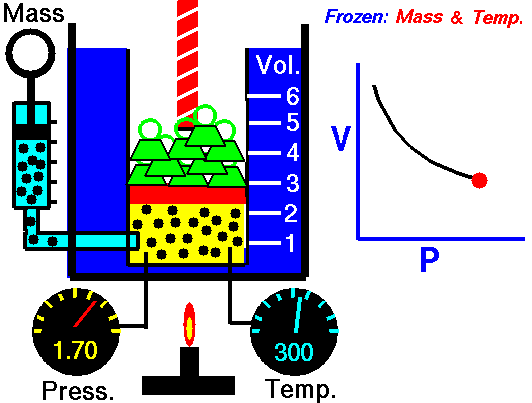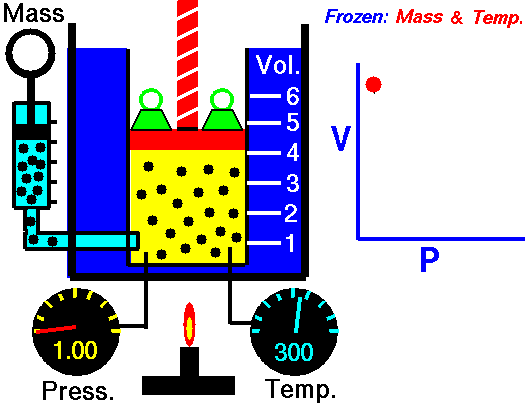
Entonces cuando nos enfrentemos a un problema de este tipo, lo primero que se debe hacer el buscar la fórmula y observar la relación proporcional entre las variables.
Nota: Todos los problemas de proporcionalidad se pueden resolver por demostración también y casi todos los de demostración se pueden resolver por el método de “números pequeños” recién explicado, así es que ahora disponen de dos herramientas poderosas.
Ahora, debes realizar una práctica, que se encuentra aquí:
¿Y por que es útil un tema tan simple?
Porque comprender que si el aumento de una variables está en el denominador (abajo de una división) nos origina un resultado menor, o que si está en el numerador, el aumento de la variable nos originarán un aumento en el resultado, es una herramienta de solución de problemas complejos con facilidad, por ejemplo, en este problema que solucionó en el tema anterior de demostraciones:
- En un tomacorriente de voltaje V, se conecta un aparato eléctrico con resistencia R, en el cual circula una corriente I. Suponga que este mismo artefacto se pudiera conectar a un tomacorriente cuyo voltaje es 2 V y aun así funcionaría, entonces, la nueva corriente eléctrica que circularía por el artefacto, con respecto a la inicial, sería
| a) igual | b) el doble | c) la mitad | d) el cuádruplo |
Sabemos que la fórmula para resolverlo es: I= V.R por lo tanto hay proporción directa entre la intensidad y el voltaje, si se aumenta el voltaje, la intensidad aumenta, por lo tanto, partiendo del concepto de proporcionalidad discrimino y ahora tengo 50% de probabilidades de acertar: b o d.
Otra situación en otro tema:
- Un satélite orbita un planeta de masa m, a una distancia r desde el centro de dicho planeta, con una rapidez constante v. Suponga que el planeta, repentinamente, experimenta una disminución de su masa, a la cuarta parte de m; si el radio de la órbita r no varía, entonces, respecto a la rapidez inicial del satélite, la nueva rapidez del satélite
a) aumenta el doble b) disminuye a la mitad c) aumenta cuatro veces d) disminuye a la cuarta parte
La fórmula que se usa es
Al explorar la fórmula vemos que la velocidad y masa son directamente proporcionales, por lo tanto al disminuir la masa (como las otras variables no varían) entonces la velocidad orbital debe disminuir, entonces ya hemos descartado el 50% de opciones y nos quedamos solo con las opciones b y d.
Pero si pensamos un poco más, dice el enunciado que disminuye la cuarta parte, eso es 1/4 y como hay que sacar raíz cuadrada queda, entonces Raíz de 1/4 = 0,5, por lo tanto la respuesta será b.
Así es que obtuvimos la respuesta por un proceso más corto que por demostración.
Es probable que en este punto usted esté pensando que esta herramienta es fantástica, pues con ella ya es posible solucionar problemas demostrativos sin requerir hacer una demostración compleja, bueno, eso no es así, hay ejercicios como el siguiente que requieren la demostración para obtener la fórmula con que se trabajará y posterior a eso, si es posible averiguarlo por proporcionalidad, pero ya en ese punto la respuestas estará casi dada, por ejemplo este caso:
- Saturno, cuyo radio ecuatorial es r, atrae a un satélite que orbita a una radio 3r, con una fuerza gravitacional de magnitud F. Si a otro satélite idéntico la atrae con una fuerza 4F, entonces, el nuevo radio a que se encuentra desde el centro de Saturno es
| a) r | b) 2r | c) 0,5 r | d) 1,5 r |
Esta misma limitación de utilizar proporcionalidades para solución rápida de ejercicios la encontramos cuando en el ejercicios no hablan del cambio en varias variables en numerador y denominador.
Así es que se ha aprendido el uso de una herramienta de solución de problemas, pero es una herramienta limitada, aunque muy rápida e intuitiva.
Este tema está relacionado con Demostraciones, si quieres refrescar qué son demostraciones, ve a esta lección:
