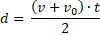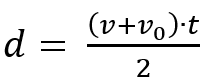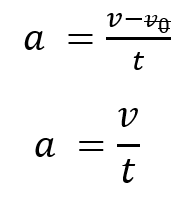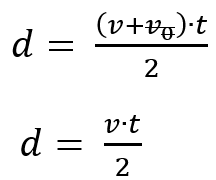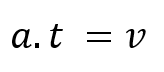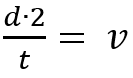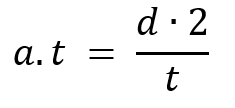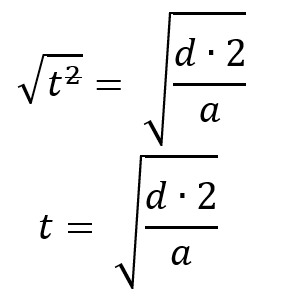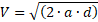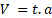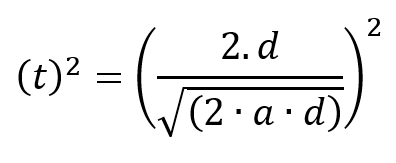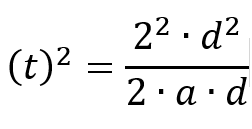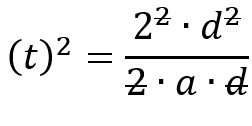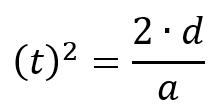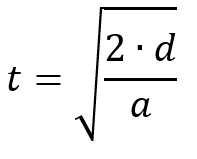Demostraciones
Saber hacer demostraciones es una habilidad indispensable para la física y por tanto todo físico, ingeniero, topógrafo, arquitecto, etc.. debe conocer y manejar esta herramienta intelectual.
Seguidamente se exponen demostraciones en varios temas, por eso, en una misma página encontrará información suficiente para comprender este tema completamente.
Vídeo que explica demostraciones, este video es más amplio que este texto, y además explica otra habilidad importante en física que va de la mano de demostraciones (proporcionalidades), dura una hora:
Demostraciones en el tema de Caída Libre
Introducción a las Demostraciones:
Hay muchos tipos de demostraciones en física, algunas veces se le llama demostración a un experimento, otras veces a una actividad donde se evidencia el fenómeno de estudio, etc.
En este punto veremos cómo hacer demostraciones lógico-matemáticas en física, una demostración es una habilidad imprescindible en física y posteriormente en ingenierías.
Una demostración primeramente es una comparación entre dos situaciones que bajo ciertas condiciones son iguales, por eso siempre se compara o igualan dos situaciones y se “justifica la igualdad mediante enunciados, supuestos y algebra”.
Por ejemplo:
Demuestre que es posible conocer el tiempo de caída si solamente nos dan la altura a la que está un objeto que ha partido del reposo en caída libre.
Sigamos estos pasos:
A. Busque la(s) fórmula(s) que se aplica(n) al caso de acuerdo con los datos.
B. Despeje una variable que NO le den en el ítem y sea igual en ambos casos.
C. Elabore una igualdad sustituyendo con las variables del ítem.
D. Resuelva lo que le piden despejando.
Entonces.
A. Busque la(s) fórmula(s) que se aplica(n) al caso de acuerdo con los datos
Al observar el juego de fórmulas de caída libre, notamos que solo tenemos una fórmula de tiempo, por eso la usaremos, pero como ocuparemos llegar a una fórmula de tiempo que tenga distancia, buscaremos entre el juego de fórmulas alguna que tenga la variables del enunciado y distancia, hay varias posibilidades y con cualquiera (bien elegida) llegaremos al mismo resultado, pero con algunas parejas nos costará mucho más, por ejemplo, veamos la comparación entre dos demostraciones con diferentes juegos de fórmulas que llegan al mismo resultado, pero una simple y la otra compleja.
Como el enunciado dice: “Demuestre que es posible conocer el tiempo de caída si solamente nos dan la altura a la que está un objeto que ha partido del reposo en caída libre.” Buscamos la fórmula de tiempo y la segunda deberá tener como mínimo distancia (altura) y velocidad inicial (ya que nos dicen que parte del reposo), entonces podremos seguir estos dos procesos:
|
Forma 1 de resolverlo |
Forma 2 de resolverlo |
||||||||||||
|
Ahora elegimos este conjunto de fórmulas:
Notemos que el ítem dice que se parte del reposo, por eso eliminamos la velocidad inicial de ambas ecuaciones, quedando:
B. Despeje una variable que NO le den en el ítem y sea igual en ambos casos.
Nos piden averiguar el tiempo, por lo tanto, lo despejamos: 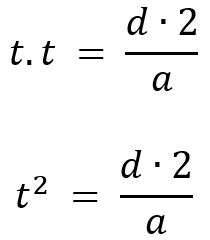
Resolvemos metiendo raíz a ambos lados, la cual me cancela el cuadrado de la izquierda y a la derecha queda todo en raíz: |
Partimos de la fórmula de tiempo y la exploramos, e igual exploremos la fórmula de velocidad final. Como el objeto parte del reposo, la velocidad inicial es cero; entonces puedo eliminarla de las fórmulas iniciales quedando así:
B) Despeje una variable que NO le den en el ítem y sea igual en ambos casos. En el ítem solo le hablan de tiempo y altura (distancia), ahora, observemos que la velocidad final (V) no va a cambiar en ambos casos, así es que la despejamos:
Elabore una igualdad sustituyendo con las variables del ítem. 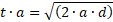 Resuelva lo que le piden despejando. 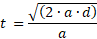 Simplificamos el radical recordando que para simplificarlo debemos multiplicar el radical dos veces por la misma expresión, quedando así: 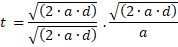 Resuelvo: 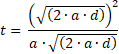 En el numerador (arriba), cancelo el cuadrado con la raíz cuadrada quedando 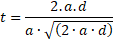 Ahora puedo cancelar las dos “a” quedando como resultado esto: 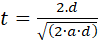 Nota: Observe que no podemos cancelar la “a” dentro de la raíz. Una “a” cancela solo una “a”. Esta expresión podemos simplificarla aún más, si elevamos al cuadrado a ambos lados, con lo que conseguiré cancelar la raíz de abajo: |
Como pueden ver, ambas formas de resolverlo dan el mismo resultado, pero la forma 2 es mucho más larga y complicada.
Entonces: ¿Cómo saber cuál par de fórmulas escoger y es la mejor?
No hay forma de saberlo, pero si todas deben dar igual, unas serán más complicadas que otras, pero darán el mismo resultado, SI SE HAN ELEGIDO las fórmulas correctas.
— — — — — — — — — — — — —
Vamos a ver si ha comprendido, resuelva el siguiente ejercicio:
Demuestre que
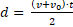
Es el resultado de trabajar éstas otras dos fórmulas:
| Ecuación 1: | Ecuación 2: |
Nota: para solucionarlo debes recordar estos dos aspectos:
2) la segunda fórmula notable:
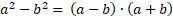
| Este espacio es para que resuelva:
|
Respuesta a la demostración:
a) Busque la(s) fórmula(s) que se aplica(n) al caso de acuerdo con los datos. Ya nos las dan.
b)Despeje una variable que NO le den en el ítem y sea igual en ambos casos.
Como buscamos una fórmula que no tiene “a”, entonces en la segunda ecuación despejo “a”
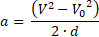
c) Elabore una igualdad sustituyendo con las variables del ítem.
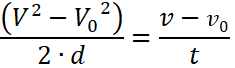 |
d) Resuelva lo que le piden despejando.
Aquí deben despejar d:
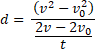
Aquí puedo multiplicar el dos, resultando así:
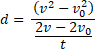
Observo de debajo del numerador ( ![]() ) hay un uno imaginario:
) hay un uno imaginario:
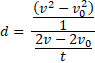
Ahora resuelvo esa expresión multiplicando extremos por extremos y medios por medios resultando:
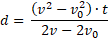
Ahora puedo factorizar, por factor común, el 2
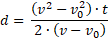
En este punto no tengo otra opción más que descomponer el numerador que tiene forma de la segunda fórmula notable: ![]()
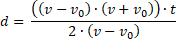
Ahora, observe que las expresiones (V-V0) están repetidas abajo y arriba y están multiplicando, por lo tanto, puedo eliminarlas quedando finalmente así: