Solución de problemas simbólicos
En esta lección hay dos videos que explican el mismo tema, el primer video se refiere al PDF que seguidamente encuentra, y explica en mejor detalle, además de que explica tres métodos.
Video de la explicación de este tema: https://www.fisicalinda.com/download/3-metodos-de-solucion-de-problemas-simbolicos-o-no-numericos/
Este otro video de abajo explica también el mismo tema, pero con solo con dos métodos de los tres explicados en el video de arriba:
Un problema simbólico es aquel en el que solo se trabaja con variables.
Por ejemplo:
Un satélite artificial está en una órbita circular de radio R, alrededor de un planeta y con velocidad tangencial de magnitud v. Si se cambia a una órbita en la que la magnitud de la nueva velocidad es 2 v, ¿Cuál es el radio de esta órbita?
a) R / 2
b) R / 4
c) 2 R
d) 4 R
¿Cuál es la variación en la densidad de un cuerpo que se mantiene constante su masa pero se le aplica una fuerza tal que disminuye su volumen 1/5?
¿Qué velocidad alcanza una partícula que originalmente estaba a un radio r si luego se le coloca en un radio 5r sin variar su frecuencia?
Seguidamente se le ofrecen dos estrategias diferentes para resolver problemas simbólicos, aquellos en los que solo trabajan con las variables de una fórmula.
Por el método de “Proporcionalidades” y por el método de “demostraciones”. En ambos métodos observe que se debe establecer dos situaciones, una inicial y otra final.
Proporcionalidades
Ya habíamos estudiado proporcionalidades (https://www.fisicalinda.com/lessons/proporcionalidades/) pero ahora las repasamos y aplicamos específicamente para este tipo de problemas.
Proporcionalidades es otra de las habilidades importantes en física.
Cuando hablamos de proporcionalidades, nos referimos a la forma como dos valores o variables (distancia con tiempo, velocidad con aceleración y otros) se relacionan entre sí, y tenemos dos tipos:
Proporción directa y proporción inversa.
Proporción directa:
Si al aumentar una variable el resultado aumenta o si al disminuir una variable el resultado disminuye en la misma proporción, es una situación de proporción directa.
Por ejemplo:
En la fórmula: ![]() la meje es directamente proporcional a la velocidad. Si aumento masa, aumenta velocidad. Puede probarlo con números y verá que se cumple.
la meje es directamente proporcional a la velocidad. Si aumento masa, aumenta velocidad. Puede probarlo con números y verá que se cumple.
Proporción inversa:
Si al aumentar una variable el resultado disminuye, o si al disminuir la variable el resultado aumenta en la misma proporción, es una situación de proporción inversa.
Por ejemplo:
En la fórmula:
![]() el “r” es inversamente proporcional a la velocidad. Si aumento radio, velocidad disminuye.
el “r” es inversamente proporcional a la velocidad. Si aumento radio, velocidad disminuye.
Una forma de probar la proporcionalidad es usar números pequeños (quizá sustituir por uno en todo lado) en la fórmula, y hacer el cambio respectivo que el ítem les dice, por ejemplo:
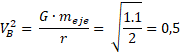 ¿Cuáles satélites giran más rápido, los que están cerca del eje de rotación o los que están lejos del eje de rotación?
¿Cuáles satélites giran más rápido, los que están cerca del eje de rotación o los que están lejos del eje de rotación?
1) Identifica las variables de las que le hablan en el ítem y busca la fórmula que podría resolver el ítem. En este caso las variables son velocidad y radio.
2) Establece dos casos, el primero será solo para comparar qué ocurre al cambiar la variable que el ítem le indica.
Use números inventados y pequeños por facilidad, en el caso “A” utilice un período de 1s y en el caso B un período de 2s.
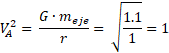
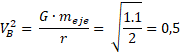
3) Responde: Como se ve en este caso la velocidad de los que están más lejos (con radio 2) es menor.
Práctica:
1) A) ¿La fuerza de atracción gravitacional es directa o inversamente proporcional al radio a que se encuentre el cuerpo del centro terrestre?
Respuesta: De la ecuación: ![]() se observa que radio está abajo, por eso es inversamente proporcional al radio.
se observa que radio está abajo, por eso es inversamente proporcional al radio.
- Si aumentamos la distancia de separación entre la tierra y el cuerpo, ¿qué ocurre con la fuerza?
Respuesta: Disminuye la fuerza, porque el radio es inversamente proporcional a la fuerza.
2) a) Cuál es la proporción existente entre la masa de los cuerpos y la fuerza gravitacional que experimentan?
- b) ¿Cuándo aumento la masa de un cuerpo, experimenta más o menos fuerza gravitacional? Explique su respuesta.
Demostraciones para resolver problemas no numéricos
En física con frecuencias se usan problemas simbólicos o no numéricos para averiguar la relación entre las variables, por ejemplo:
Un satélite artificial está en una órbita circular de radio R, alrededor de un planeta y con velocidad tangencial de magnitud v. Si se cambia a una órbita en la que la magnitud de la nueva velocidad es 2 v, ¿cuál es el radio de esta órbita?
| a) R / 2 | b) R / 4 | c) 2 R | d) 4 R |
Primeramente, observe que nos dan dos situaciones, una inicial y otra final, por eso, podemos establecer una igualdad.
Entonces sigamos estos pasos:
- Busque la(s) fórmula(s) que se aplica(n) al caso de acuerdo con los datos.
- Despeje una variable que NO le den en el ítem y sea igual en ambos casos.
- Elabore una igualdad sustituyendo con las variables del ítem.
- Resuelva lo que le piden despejando.
Aplicando estos pasos al ítem anterior, quedaría así:
- Busque la(s) fórmula(s) que se aplica(n) al caso de acuerdo con los datos.
Aquí los datos que ofrecen son: Radio, Velocidad tangencial. ¿Cuál fórmula tiene esos datos?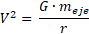
nota: se podría usar cualquier fórmula con esas variables, por ejemplo, también podríamos pensar que nos funcionan:
| Pero usar esta nos produce un error al final debido a que las fuerzas centrípetas no son iguales con velocidad V y 2V. | Usar esta fórmula también nos da un error porque el periodo no es igual cuando tiene velocidad V que cuando es 2V. |
- Despeje una variable que NO le den en el ítem y sea igual en ambos casos. Ya que le dan la velocidad y radio, entonces se despeja cualquiera de las variables que no le dan, por ejemplo, despeje meje:
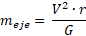
- Elaboro una igualdad con las variables (una demostración):
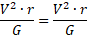
Sustituya en la fórmula de acuerdo con la información provista. En este ítem me dicen:
“Un satélite artificial está en una órbita circular de radio R, alrededor de un planeta y con velocidad tangencial de magnitudv. Si se cambia a una órbita en la que la magnitud de la nueva velocidad es 2 v, ¿cuál es el radio de esta órbita?”
De modo que ahora buscaremos cambiar a 2v en alguno de los lados, lo haremos al lado derecho:
![]()
- Resuelva lo que le piden despejando. En este ítem le piden el radio, entonces despejamos radio quedando así:
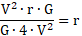
Cancelo todos los que son iguales:
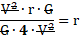
Resultando:
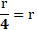
Ahora volviendo al ítem, ¿cuál diría usted que es la respuesta?
Un satélite artificial está en una órbita circular de radio R, alrededor de un planeta y con velocidad tangencial de magnitud v. Si se cambia a una órbita en la que la magnitud de la nueva velocidad es 2 v, ¿cuál es el radio de esta órbita?
| a) R / 2 | b) R / 4 | c) 2 R | d) 4 R |
R/ b |
Estudiemos otro ítem, pero del tema de IV Ley de Newton:
Dos personas con masas iguales se atraen con una fuerza gravitatoria de magnitud F. Si la distancia de separación entre ellas se reduce a la mitad, la nueva fuerza de atracción tendrá una magnitud igual a
| a) 2 F | b) 4 F | c) F / 2 | d) F / 4 |
Sigamos los cuatro pasos anteriores:
- Busque la(s) fórmula(s) que se aplica(n) al caso de acuerdo con los datos.
![]()
- Despeje una variable que NO le den en el ítem y sea igual en ambos casos.
Como no le dan G, por eso lo despejaremos:![]()
- Elabore una igualdad sustituyendo con las variables del ítem.
![]()
Ahora vamos a sustituir en la igualdad con las variables o datos del ítem:
El ítem dice: “Si la distancia de separación entre ellas se reduce a la mitad”. Así es que ahora en alguno de los dos lados debemos hacer la distancia (radio) a la mitad (dividir entre 2), aquí lo haremos en el radio al lado derecho:
| OJO, dice que la distancia se reduce a la mitad, ya que la ecuación tiene el radio al cuadrado, debo elevar al cuadrado la fracción r/2 | ERROR: Si lo haces como está abajo en esta columna, esto es un error, pues aquí solo estás elevando al cuadrado el radio simple. Observe que el ítem dice que la distancia se reduce a la mitad. |
Resuelva lo que le piden despejando.
En el ítem le piden: “la nueva fuerza de atracción tendrá una magnitud igual a:” por lo tanto se debe despejar la fuerza en el mismo lado donde se hizo el cambio:
Observe, que para simplificar el proceso aquí se elevó al cuadrado cada término de ![]()
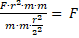
Es más fácil si primero se resuelve y luego se cancela. Como es una fracción abajo, agregamos arriba un uno y ahora hay dos fracciones, que las resolvemos multiplicando medios por medios y extremos por extremos:
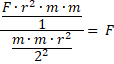
Resolvemos multiplicando extremos por extremos y medios por medios:
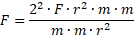
Y cancelo:
![]()
Resultando: F=22 .F
Entonces volviendo al ítem, ¿cuál será la respuesta?
Dos personas con masas iguales se atraen con una fuerza gravitatoria de magnitud F. Si la distancia de separación entre ellas se reduce a la mitad, la nueva fuerza de atracción tendrá una magnitud igual a
| a) 2 F | b) 4 F | c) F / 2 | d) F / 4 | R/ b |
